domicile » Chauffage dans la maison » La notation intégrale de la formule de Newton - intégrale de Leibniz est utilisée. Calculatrice en ligne Calculer l'intégrale définie (aire d'un trapèze courbe)

La notation intégrale de la formule de Newton - intégrale de Leibniz est utilisée. Calculatrice en ligne Calculer l'intégrale définie (aire d'un trapèze courbe)

Considérons une fonction. Cette fonction est appelée : intégrale en fonction de la borne supérieure. Notons plusieurs propriétés de cette fonction.
Théorème 2.1. Si f (x) est une fonction intégrable, alors Ф (x) est continue sur.
Preuve... Par la propriété 9 de l'intégrale définie (théorème de la valeur moyenne) nous avons , d'où, car, nous obtenons ce qui est requis.
Théorème 2.2. Si f (x) est continue sur une fonction, alors Ф '(x) = f (x) sur.
Preuve... Par la propriété 10 de l'intégrale définie (le deuxième théorème de la valeur moyenne), on a où avec- un point du segment. Puisque la fonction f est continue, on obtient
Ainsi, (x) est l'une des primitives de la fonction f (x), donc Ф (x) = F (x) + C, où F (x) est une autre primitive de f (x). De plus, puisque Ф (a) = 0, alors 0 = F (a) + C, donc, C = -F (a) et donc Ф (x) = F (x) - F (a). En fixant x = b, on obtient la formule de Newton-Leibniz

Exemples de
1.

Intégration par parties dans une intégrale définie

Dans une intégrale définie, la formule d'intégration par parties est conservée. Dans ce cas, il prend la forme

Exemple.

Changement de variables dans une intégrale définie

Une des variantes des résultats sur le changement de variables dans une intégrale définie est la suivante.
Théorème 2.3. Soit f (x) continue sur un intervalle et satisfait aux conditions :
1) (α) = un
2) (β) = b
3) la dérivée φ ’(t) est définie partout sur le segment [α, β]
4) pour tout t de [α, β]
Puis

Preuve. Si F (x) est une primitive pour f (x) dx alors F (φ (t)) est une primitive pour Donc, F (b) - F (a) = F (φ (β)) - F (φ (α) ). Le théorème est démontré.
Commenter. Si la continuité de la fonction f (x) est abandonnée dans les conditions du théorème 2.3, il faut exiger la monotonie de la fonction φ (t).

Exemple. Calculer l'intégrale On pose Alors dx = 2tdt et donc

Problème 1(à propos du calcul de l'aire trapèze courbe).

Dans le système de coordonnées rectangulaires cartésiennes xOy, une figure est donnée (voir figure), délimitée par l'axe des x, par des droites x = a, x = b (a par un trapèze courbe. Il est nécessaire de calculer l'aire de un trapèze courbe.
Solution. La géométrie nous donne des recettes pour calculer les aires des polygones et certaines parties d'un cercle (secteur, segment). En utilisant des considérations géométriques, nous ne pourrons trouver qu'une valeur approximative de la surface requise, en argumentant comme suit.

Nous divisons le segment [a; b] (base d'un trapèze courbe) par n parts égales; cette partition est réalisable en utilisant les points x 1, x 2, ... x k, ... x n-1. Traçons des lignes droites passant par ces points parallèlement à l'axe des y. Ensuite, le trapèze curviligne donné sera divisé en n parties, en n colonnes étroites. L'aire de tout le trapèze est égale à la somme des aires des colonnes.

Considérez la k-ième colonne séparément, c'est-à-dire un trapèze curviligne dont la base est un segment. Remplaçons-le par un rectangle de même base et de hauteur égale à f (x k) (voir figure). L'aire du rectangle est $f(x_k)\cdot\Delta x_k$, où $\Delta x_k$ est la longueur du segment; il est naturel de considérer le produit compilé comme une valeur approximative de l'aire de la k-ème colonne.

Si on fait maintenant de même avec toutes les autres colonnes, on arrivera au résultat suivant : l'aire S d'un trapèze curviligne donné est approximativement égale à l'aire S n d'une figure en escalier composée de n rectangles (voir figure) :
\ (S_n = f (x_0) \ Delta x_0 + \ points + f (x_k) \ Delta x_k + \ points + f (x_ (n-1)) \ Delta x_ (n-1) \)
Ici, par souci d'uniformité de notation, nous supposons que a = x 0, b = x n ; \ (\ Delta x_0 \) - longueur du segment, \ (\ Delta x_1 \) - longueur du segment, etc. en même temps, comme convenu plus haut, \ (\ Delta x_0 = \ points = \ Delta x_ (n-1) \)

Donc, $S\approx S_n$, et cette égalité approchée est d'autant plus précise, plus n est grand.
Par définition, on suppose que l'aire requise d'un trapèze curviligne est égale à la limite de la suite (S n) :
$$ S = \ lim_ (n \ à \ infty) S_n $$

Tâche 2(à propos du point mobile)
Un point matériel se déplace en ligne droite. La dépendance de la vitesse au temps est exprimée par la formule v = v (t). Trouver le déplacement d'un point sur une période de temps [a; b].
Solution. Si le mouvement était uniforme, alors le problème serait résolu très simplement : s = vt, c'est-à-dire s = v (b-a). Pour un mouvement inégal, vous devez utiliser les mêmes idées sur lesquelles la solution du problème précédent était basée.
1) Divisez l'intervalle de temps [a; b] en n parties égales.
2) Considérons un intervalle de temps et supposons que pendant cet intervalle de temps, la vitesse était constante, comme au temps t k. On considère donc que v = v (t k).
3) Trouver la valeur approximative du déplacement du point sur une période de temps, cette valeur approximative sera notée s k
\ (s_k = v (t_k) \ Delta t_k \)
4) Trouver la valeur approximative du déplacement s :
\ (s \ env S_n \) où
\ (S_n = s_0 + \ points + s_ (n-1) = v (t_0) \ Delta t_0 + \ points + v (t_ (n-1)) \ Delta t_ (n-1) \)
5) Le déplacement souhaité est égal à la limite de séquence (S n) :
$$ s = \ lim_ (n \ à \ infty) S_n $$

Résumons. Les solutions à divers problèmes ont été réduites au même modèle mathématique. De nombreux problèmes issus de divers domaines de la science et de la technologie conduisent dans le processus de résolution au même modèle. Par conséquent, ce modèle mathématique doivent être spécialement étudiés.

Concept intégral définitif

Donnons une description mathématique du modèle qui a été construit dans les trois problèmes considérés pour la fonction y = f (x), continue (mais pas nécessairement non négative, comme cela a été supposé dans les problèmes considérés) sur l'intervalle [a; b] :
1) on divise le segment [a; b] en n parties égales ;
2) faire la somme $$ S_n = f (x_0) \ Delta x_0 + f (x_1) \ Delta x_1 + \ points + f (x_ (n-1)) \ Delta x_ (n-1) $$
3) calculer $$ \ lim_ (n \ à \ infty) S_n $$

Au cours de l'analyse mathématique, il a été prouvé que cette limite existe dans le cas d'une fonction continue (ou continue par morceaux). Il est appelé une intégrale définie de la fonction y = f (x) le long du segment [a; b] et noté comme suit :
\ (\ int \limites_a ^ b f (x) dx \)
Les nombres a et b sont appelés limites d'intégration (respectivement inférieure et supérieure).

Revenons aux tâches décrites ci-dessus. La définition de l'aire donnée dans le problème 1 peut maintenant être réécrite comme suit :
\ (S = \int \limites_a ^ b f (x) dx \)
ici S est l'aire du trapèze courbe représenté sur la figure ci-dessus. C'est sens géométrique d'une intégrale définie.

La définition du déplacement s d'un point se déplaçant en ligne droite avec une vitesse v = v (t) sur l'intervalle de temps de t = a à t = b, donnée dans le problème 2, peut être réécrite comme suit :

Formule de Newton - Leibniz

Pour commencer, répondons à la question : quel est le lien entre une intégrale définie et une primitive ?

La réponse se trouve dans le problème 2. D'une part, le déplacement s d'un point se déplaçant en ligne droite avec une vitesse v = v (t) sur l'intervalle de temps de t = a à t = b et est calculé par la formule
\ (S = \int \limites_a ^ b v (t) dt \)

D'autre part, la coordonnée du point mobile est la primitive de la vitesse - notons-la s (t) ; par conséquent, le déplacement s est exprimé par la formule s = s (b) - s (a). En conséquence, nous obtenons :
\ (S = \int \limites_a ^ b v (t) dt = s (b) -s (a) \)
où s (t) est la primitive de v (t).

Au cours de l'analyse mathématique, le théorème suivant a été prouvé.
Théorème. Si la fonction y = f (x) est continue sur le segment [a; b], alors la formule suivante est valide
\ (S = \int \limites_a ^ b f (x) dx = F (b) -F (a) \)
où F (x) est la primitive de f (x).

La formule ci-dessus est généralement appelée par la formule Newton - Leibniz en l'honneur du physicien anglais Isaac Newton (1643-1727) et philosophe allemand Gottfried Leibniz (1646-1716), qui l'ont reçu indépendamment les uns des autres et presque simultanément.

En pratique, au lieu d'écrire F (b) - F (a), utilisez la notation \ (\ left. F (x) \ right | _a ^ b \) (parfois appelée double substitution) et, en conséquence, réécrivez la formule de Newton - Leibniz sous la forme suivante :
\ (S = \ int \limits_a ^ b f (x) dx = \ left. F (x) \ right | _a ^ b \)

Pour calculer une intégrale définie, trouvez d'abord la primitive, puis effectuez une double substitution.

Sur la base de la formule de Newton - Leibniz, deux propriétés d'une intégrale définie peuvent être obtenues.

Propriété 1. L'intégrale de la somme des fonctions est égale à la somme des intégrales :
\ (\int \limites_a ^ b (f (x) + g (x)) dx = \int \limites_a ^ b f (x) dx + \int \limites_a ^ b g (x) dx \)

Propriété 2. Le facteur constant peut être retiré du signe intégral :
\ (\ int \limites_a ^ b kf (x) dx = k \ int \limites_a ^ b f (x) dx \)

Calcul des aires de figures planes à l'aide d'une intégrale définie

En utilisant l'intégrale, il est possible de calculer les aires non seulement de trapèzes curvilignes, mais également de figures planes d'un type plus complexe, par exemple celui représenté sur la figure. La figure P est bornée par des droites x = a, x = b et des graphes de fonctions continues y = f (x), y = g (x), et sur le segment [a; b] l'inégalité \ (g (x) \ leq f (x) \) est vraie. Pour calculer l'aire S d'une telle figure, on procédera comme suit :
\ (S = S_ (ABCD) = S_ (aDCb) - S_ (aABb) = \ int \limits_a ^ b f (x) dx - \ int \limits_a ^ b g (x) dx = \)
\ (= \ int \limites_a ^ b (f (x) -g (x)) dx \)

Ainsi, l'aire S de la figure délimitée par les droites x = a, x = b et les graphes des fonctions y = f (x), y = g (x), continues sur le segment et telles que pour tout x du segment [a; b] l'inégalité \ (g (x) \ leq f (x) \) est vérifiée, calculée par la formule
\ (S = \int \limites_a ^ b (f (x) -g (x)) dx \)

Tableau des intégrales indéfinies (dérivées) de certaines fonctions

$$ \ int 0 \ cdot dx = C $$ $$ \ int 1 \ cdot dx = x + C $$ $$ \ int x ^ n dx = \ frac (x ^ (n + 1)) (n + 1 ) + C \; \; (n \ neq -1) $$ $$ \ int \ frac (1) (x) dx = \ ln | x | + C $$ $$ \ int e ^ x dx = e ^ x + C $$ $$ \ int a ^ x dx = \ frac (a ^ x) (\ ln a) + C \; \; (a> 0, \; \; a \ neq 1) $$ $$ \ int \ cos x dx = \ sin x + C $$ $$ \ int \ sin x dx = - \ cos x + C $$ $ $ \ int \ frac (dx) (\ cos ^ 2 x) = \ text (tg) x + C $$ $$ \ int \ frac (dx) (\ sin ^ 2 x) = - \ text (ctg) x + C $$ $$ \ int \ frac (dx) (\ sqrt (1-x ^ 2)) = \ text (arcsin) x + C $$ $$ \ int \ frac (dx) (1 + x ^ 2 ) = \ text (arctg) x + C $$ $$ \ int \ text (ch) x dx = \ text (sh) x + C $$ $$ \ int \ text (sh) x dx = \ text (ch ) x + C$$

Aperçu:

Pour utiliser l'aperçu des présentations, créez vous-même un compte Google (compte) et connectez-vous : https://accounts.google.com

Légendes des diapositives :

Intégral. Formule de Newton - Leibniz. compilé par: professeur de mathématiques GUNPO PU No. 27 p. Shchelyayur Semyashkina Irina Vasilievna

Objectif de la leçon : Introduire le concept d'intégrale et son calcul selon la formule de Newton - Leibniz, en utilisant la connaissance de la primitive et les règles de son calcul ; Illustrer l'application pratique de l'intégrale par des exemples de recherche de l'aire d'un trapèze courbe ; Consolider ce qui a été appris lors des exercices.

Définition : Soit une fonction positive f (x) définie sur un segment fini [a; b]. L'intégrale de la fonction f(x) sur [a;b] est l'aire de son trapèze curviligne. y = f (x) b a 0 x y

Désignation :  "intégrale de a à b eff de x de x"

Référence historique: Leibniz a dérivé la notation intégrale de la première lettre du mot Summa. Newton dans ses œuvres n'a pas proposé de symbolisme alternatif de l'intégrale, bien qu'il ait essayé différentes options... Le terme intégral lui-même a été inventé par Jacob Bernoulli. S umma Isaac Newton Gottfried Wilhelm von Leibniz Jacob Bernoulli

Euler a introduit la notation intégrale indéfinie. Jean Baptiste Joseph Fourier Leonard Euler Fourier a proposé la conception de l'intégrale définie sous la forme à laquelle nous sommes habitués.

Formule de Newton - Leibniz

Exemple 1. Calculer l'intégrale définie : = Solution :

Exemple 2. Calculer les intégrales définies : 5 9 1

Exemple 3. S y x Calculer l'aire de la figure délimitée par des lignes et l'abscisse. Cherchons d'abord les points d'intersection de l'axe des abscisses avec le graphe de la fonction. Pour ce faire, résolvons l'équation. = Résolution : S =

y x S A B D C Exemple 4. Calculer l'aire de la figure délimitée par les droites et Trouver les points d'intersection (abscisses) de ces droites en résolvant l'équation S = S BADC - S BAC S BADC = = S BAC = S = 9 - 4,5 = 4,5 voir exemple 1 Solution :

REGLES SYNQUWINE 1 ligne - sujet syncwine 1 mot 2 ligne - 2 adjectifs décrivant les caractéristiques et les propriétés du sujet 3 lignes - 3 verbes décrivant la nature de l'action 4 lignes - une courte phrase de 4 mots, montrant votre attitude personnelle vis-à-vis du sujet 5 ligne - 1 mot, synonyme ou sujet de votre sujet d'association ...

Intégrale 2. Défini, positif Compter, additionner, multiplier 4. Calculer par la formule de Newton - Leibniz 5. Aire

Liste de la littérature utilisée : manuel Kolmagorov A.N. et autres Algèbre et début d'analyse 10 - 11 cl.

Merci pour l'attention! "LE TALENT est 99% de travail et 1% de capacité" sagesse populaire

Exemple 1. Calculer l'intégrale définie : = Solution : exemple 4

Aperçu:

Sujet : mathématiques (algèbre et le début de l'analyse), année : 11e année.

Sujet de la leçon : "Intégral. Formule de Newton-Leibniz".

Type de cours : Apprentissage de nouveau matériel.

Durée de la leçon : 45 minutes.

Objectifs de la leçon: introduire le concept d'intégrale et son calcul selon la formule de Newton-Leibniz, en utilisant la connaissance de la primitive et les règles de son calcul ; illustrer l'application pratique de l'intégrale par des exemples de recherche de l'aire d'un trapèze curviligne ; consolider ce qui a été appris au cours de l'exercice.

Objectifs de la leçon:

Éducatif:

former le concept d'intégrale;
développer des compétences pour calculer une intégrale définie;
formation de compétences application pratique intégrale pour trouver l'aire d'un trapèze curviligne.

Développement:

le développement de l'intérêt cognitif des étudiants, pour développer le discours mathématique, la capacité d'observer, de comparer, de tirer des conclusions;
développer l'intérêt pour le sujet en utilisant les TIC.

Éducatif:

intensifier l'intérêt pour l'obtention de nouvelles connaissances, la formation de l'exactitude et de l'exactitude dans le calcul de l'intégrale et la réalisation de dessins.

Équipement: ordinateur, système opérateur Programme Microsoft Windows 2000 / XP, MS Office 2007 : Power Point, Microsoft Word; projecteur multimédia, écran.

Littérature: manuel Kolmagorov A.N. et autres.Algèbre et le début de l'analyse des 10-11 grades.

Technologies : TIC, formation individuelle.

PENDANT LES COURS

Étape de la leçon	Activité de l'enseignant	Activités étudiantes	Temps
Partie introductive
Organisation du temps	Accueille, vérifie l'état de préparation des élèves pour le cours, organise l'attention. Distribue les notes d'accompagnement.	Écoutez, notez la date.	3 minutes
Communication du sujet et des objectifs de la leçon	Actualisation des connaissances de base et de l'expérience subjective avec une sortie aux objectifs de la leçon.	Ils écoutent, notent le sujet de la leçon dans un cahier.Ils sont activement impliqués dans l'activité mentale. Analyser, comparer, tirer des conclusions avec un résultat aux objectifs de la leçon.	Présentation TIC 3 minutes
La partie principale de la leçon Présentation du nouveau matériel avec un test d'accompagnement de la connaissance des sujets passés.
Définition intégrale (diapositive 3)	Fournit une définition. TIC Qu'est-ce qu'un trapèze courbe ?	Une figure délimitée par le graphique d'une fonction, un segment et des droites x = a et x = b.	10 minutes
Notation intégrale (diapositive 4)	Introduit la notation de l'intégrale et la façon dont elle est lue.	Ils écoutent, enregistrent.
Histoire intégrale (diapositives 5 et 6)	Raconte l'histoire du terme "intégrale".	Ils écoutent et enregistrent brièvement.
Formule Newton - Leibniz (diapositive 7)	Donne la formule de Newton-Leibniz. Que signifie F dans la formule ?	Ils écoutent, écrivent, répondent aux questions de l'enseignant. Primitive.
La dernière partie de la leçon.
Sécurisation du matériel. Résoudre des exemples en utilisant le matériel étudié
Exemple 1 (diapositive 8)	Analyse la solution d'un exemple, en posant des questions sur la recherche de primitives pour les intégrandes.	Écouter, écrire, montrer la connaissance du tableau des primitives.	20 minutes
Exemple 2 (diapositive 9). Exemples de décision indépendante apprenants.	Contrôle la résolution des exemples.	Effectuez la tâche à tour de rôle, en commentant (technologie d'apprentissage individuel), écoutez-vous les uns les autres, écrivez, montrez des connaissances sur des sujets passés.
Exemple 3 (diapositive 10)	Déconstruit l'exemple de solution. Comment trouver les points d'intersection de l'axe des abscisses avec le graphe de la fonction ?	Écoutez, répondez aux questions, montrez votre connaissance des sujets passés, écrivez. Égalisez l'intégrande à 0 et résolvez l'équation.
Exemple 4 (diapositive 11)	Déconstruit l'exemple de solution. Comment trouver les points d'intersection (abscisses) de graphes de fonctions ? Déterminer le type de triangle ABC. Comment trouver l'aire d'un triangle rectangle ?	Ils écoutent, répondent aux questions. Égalisez les fonctions les unes aux autres et résolvez l'équation résultante. Rectangulaire. où a et b sont les jambes d'un triangle rectangle.
Résumé de la leçon (diapositives 12 et 13)	Organise le travail sur la compilation de syncwine.	Participer à la compilation de syncwine. Analyser, comparer, tirer des conclusions sur le sujet.	5 minutes.
Affectation à domicile par niveau de difficulté.	Donne des devoirs, explique.	Ils écoutent, enregistrent.	1 minute.
Évaluation du travail des élèves en classe.	Évalue le travail des élèves en classe, analyse.	Ecoutez.	1 minute

Aperçu:

Notes à l'appui sur le sujet « Integral. Formule de Newton-Leibniz".

	Définition: Soit une fonction positive f (x) défini sur un segment fini.L'intégrale de la fonction f (x) surappelé l'aire de son trapèze curviligne.
	La désignation: Lire: "Intégrale de a à b eff de x de x"
	Formule de Newton - Leibniz
	Exemple 1. Calculer une intégrale définie : Solution:
	Exemple 3. et l'abscisse. Solution:
	Exemple 3. Calculer l'aire d'une forme délimitée par des lignes et .

La résolution des problèmes appliqués se réduit au calcul de l'intégrale, mais il n'est pas toujours possible de le faire avec précision. Parfois, il est nécessaire de connaître la valeur d'une intégrale définie avec un certain degré de précision, par exemple jusqu'au millième.

Il y a des problèmes lorsqu'il serait nécessaire de trouver la valeur approximative d'une certaine intégrale avec la précision requise, alors l'intégration numérique est utilisée, comme la méthode de Simposna, trapèzes, rectangles. Tous les cas ne permettent pas de le calculer avec une certaine précision.

Cet article traite de l'application de la formule de Newton-Leibniz. Ceci est nécessaire pour calculer avec précision l'intégrale définie. Des exemples détaillés seront donnés, des changements de variables dans une intégrale définie seront considérés, et nous trouverons les valeurs de l'intégrale définie lors de l'intégration par parties.

Yandex.RTB R-A-339285-1

Formule de Newton-Leibniz

Définition 1

Lorsque la fonction y = y (x) est continue à partir du segment [a; b], et F (x) est une des primitives de la fonction de ce segment, alors Formule de Newton-Leibniz considéré comme juste. Nous l'écrivons comme ∫ a b f (x) d x = F (b) - F (a).

Cette formule est considérée la formule de base du calcul intégral.

Pour prouver cette formule, il est nécessaire d'utiliser le concept d'intégrale avec une borne supérieure variable disponible.

Lorsque la fonction y = f (x) est continue à partir du segment [a; b], alors la valeur de l'argument x ∈ a ; b, et l'intégrale a la forme a x f (t) d t et est considérée comme fonction de la limite supérieure. Il faut prendre la notation de la fonction qui prendra la forme axf (t) dt = Φ (x), elle est continue, et l'inégalité de la forme ∫ axf (t) dt "= Φ" (x) = f (x) vaut pour elle.

Fixons que l'incrément de la fonction Φ (x) correspond à l'incrément de l'argument ∆ x, il faut utiliser la cinquième propriété principale de l'intégrale définie et obtenir

Φ (x + ∆ x) - Φ x = ax + ∆ xf (t) dt - ∫ axf (t) dt = = ∫ ax + ∆ xf (t) dt = f (c) x + ∆ x - x = f (c) x

où la valeur c x; x + x.

Fixons une égalité sous la forme Φ (x + ∆ x) - Φ (x) ∆ x = f (c). Par la définition de la dérivée d'une fonction, il faut passer à la limite comme ∆ x → 0, alors on obtient une formule de la forme Φ "(x) = f (x). On obtient que Φ (x) est l'une des primitives pour une fonction de la forme y = f (x), située sur [a; b]. Sinon, l'expression peut s'écrire

F (x) = (x) + C = a x f (t) d t + C, où la valeur de C est constante.

Calculons F (a) en utilisant la première propriété de l'intégrale définie. Ensuite, nous obtenons que

F (a) = Φ (a) + C = a a f (t) d t + C = 0 + C = C, on obtient donc C = F (a). Le résultat est appliqué lors du calcul de F (b) et on obtient :

F (b) = Φ (b) + C = abf (t) dt + C = ∫ abf (t) dt + F (a), autrement dit, F (b) = ∫ abf (t) dt + F (une). L'égalité prouve la formule de Newton-Leibniz a b f (x) d x + F (b) - F (a).

L'incrément de la fonction est pris comme F x a b = F (b) - F (a). A l'aide de la notation, la formule de Newton-Leibniz prend la forme a b f (x) d x = F x a b = F (b) - F (a).

Pour appliquer la formule, il est impératif de connaître l'une des primitives y = F (x) de l'intégrande y = f (x) du segment [a; b], calculez l'incrément de la primitive à partir de ce segment. Considérons quelques exemples de calculs utilisant la formule de Newton-Leibniz.

Exemple 1

Calculer l'intégrale définie 1 3 x 2 d x en utilisant la formule de Newton-Leibniz.

Solution

Considérons que l'intégrande de la forme y = x 2 est continue à partir du segment [1; 3], alors il est intégrable sur ce segment. A partir du tableau des intégrales indéfinies, nous voyons que la fonction y = x 2 a un ensemble de primitives pour toutes les valeurs réelles de x, d'où, x 1 ; 3 s'écrira F (x) = ∫ x 2 d x = x 3 3 + C. Il faut prendre la primitive avec C = 0, alors on obtient que F (x) = x 3 3.

Utilisons la formule de Newton-Leibniz et obtenons que le calcul de l'intégrale définie prendra la forme ∫ 1 3 x 2 d x = x 3 3 1 3 = 3 3 3 - 1 3 3 = 26 3.

Réponse: 1 3 x 2 d x = 26 3

Exemple 2

Calculer l'intégrale définie ∫ - 1 2 x · e x 2 + 1 d x en utilisant la formule de Newton-Leibniz.

Solution

La fonction donnée est continue à partir du segment [-1; 2], il est donc intégrable dessus. Il faut trouver la valeur de l'intégrale indéfinie ∫ x ex 2 + 1 dx en utilisant la méthode du passage sous le signe différentiel, alors on obtient ∫ x ex 2 + 1 dx = 1 2 ∫ ex 2 + 1 d (x 2 + 1) = 1 2 ex 2 + 1 + C.

On a donc un ensemble de primitives de la fonction y = x · e x 2 + 1, qui sont valables pour tout x, x ∈ - 1 ; 2.

Il faut prendre la primitive à C = 0 et appliquer la formule de Newton-Leibniz. On obtient alors une expression de la forme

∫ - 1 2 x ex 2 + 1 dx = 1 2 ex 2 + 1 - 1 2 = = 1 2 e 2 2 + 1 - 1 2 e (- 1) 2 + 1 = 1 2 e (- 1) 2 + 1 = 1 2 e 2 (e 3 - 1)

Réponse:- 1 2 x e x 2 + 1 d x = 1 2 e 2 (e 3 - 1)

Exemple 3

Calculer les intégrales ∫ - 4 - 1 2 4 x 3 + 2 x 2 d x et ∫ - 1 1 4 x 3 + 2 x 2 d x.

Solution

Segment - 4 ; - 1 2 indique que la fonction sous le signe intégral est continue, ce qui signifie qu'elle est intégrable. De là, nous trouvons l'ensemble des primitives de la fonction y = 4 x 3 + 2 x 2. On obtient ça

4 x 3 + 2 x 2 d x = 4 ∫ x d x + 2 ∫ x - 2 d x = 2 x 2 - 2 x + C

Il faut prendre la primitive F(x) = 2 x 2 - 2 x, puis, en appliquant la formule de Newton-Leibniz, on obtient l'intégrale, que l'on calcule :

∫ - 4 - 1 2 4 x 3 + 2 x 2 dx = 2 x 2 - 2 x - 4 - 1 2 = 2 - 1 2 2 - 2 - 1 2 - 2 - 4 2 - 2 - 4 = 1 2 + 4 - 32 - 1 2 = - 28

On passe au calcul de la seconde intégrale.

Du segment [- 1; 1] nous avons que l'intégrande est considéré comme non borné, car lim x → 0 4 x 3 + 2 x 2 = + ∞, alors il s'ensuit que condition nécessaire intégrabilité à partir d'un segment. Alors F (x) = 2 x 2 - 2 x n'est pas une primitive pour y = 4 x 3 + 2 x 2 du segment [- 1; 1], puisque le point O appartient au segment, mais n'est pas inclus dans le domaine de définition. Cela signifie qu'il existe une intégrale de Riemann et Newton-Leibniz définie pour la fonction y = 4 x 3 + 2 x 2 de l'intervalle [-1; 1 ] .

Réponse : ∫ - 4 - 1 2 4 x 3 + 2 x 2 d x = - 28, il existe une intégrale de Riemann et Newton-Leibniz définie pour la fonction y = 4 x 3 + 2 x 2 du segment [-1; 1 ] .

Avant d'utiliser la formule de Newton-Leibniz, vous devez connaître exactement l'existence d'une intégrale définie.

Changement d'une variable dans une intégrale définie

Lorsque la fonction y = f (x) est définie et continue à partir du segment [a; b], puis l'ensemble existant [a; b] est considérée comme la plage de valeurs de la fonction x = g (z), définie sur le segment α ; β avec la dérivée continue existante, où g (α) = a et g β = b, à partir de là on obtient que ∫ abf (x) dx = ∫ α β f (g (z)) · g "(z) d z .

Cette formule est utilisée lorsqu'il est nécessaire de calculer l'intégrale a b f (x) d x, où l'intégrale indéfinie a la forme ∫ f (x) d x, est calculée en utilisant la méthode de substitution.

Exemple 4

Calculer une intégrale définie de la forme ∫ 9 18 1 x 2 x - 9 d x.

Solution

L'intégrande est considérée comme continue sur l'intervalle d'intégration, ce qui signifie qu'une intégrale définie a lieu pour l'existence. Désignons que 2 x - 9 = z ⇒ x = g (z) = z 2 + 9 2. La valeur x = 9, signifie que z = 2 9 - 9 = 9 = 3, et pour x = 18 on obtient que z = 2 18 - 9 = 27 = 3 3, alors g α = g (3) = 9, g β = g 3 3 = 18. En substituant les valeurs obtenues dans la formule ∫ a b f (x) d x = ∫ α β f (g (z)) g "(z) d z, on obtient

9 18 1 x 2 x - 9 dx = ∫ 3 3 3 1 z 2 + 9 2 z z 2 + 9 2 "dz = = ∫ 3 3 3 1 z 2 + 9 2 z zdz = ∫ 3 3 3 2 z 2 + 9 dz

D'après le tableau des intégrales indéfinies, on a qu'une des primitives de la fonction 2 z 2 + 9 prend la valeur 2 3 a r c t g z 3. Ensuite, en appliquant la formule de Newton-Leibniz, on obtient

∫ 3 3 3 2 z 2 + 9 d z = 2 3 a r c t g z 3 3 3 3 = 2 3 a r c t g 3 3 3 - 2 3 a r c t g 3 3 = 2 3 a r c t g 3 - a r c t g 1 = 2 3 π 3 - π 4 = π 18

La recherche pourrait se faire sans utiliser la formule ∫ a b f (x) d x = ∫ α β f (g (z)) · g "(z) d z.

Si, dans la méthode de remplacement, une intégrale de la forme ∫ 1 x 2 x - 9 d x est utilisée, alors on peut arriver au résultat ∫ 1 x 2 x - 9 d x = 2 3 a r c t g 2 x - 9 3 + C.

À partir de là, nous effectuerons des calculs à l'aide de la formule de Newton-Leibniz et calculerons une intégrale définie. On obtient ça

∫ 9 18 2 z 2 + 9 dz = 2 3 arctgz 3 9 18 = = 2 3 arctan 2 18 - 9 3 - arctan 2 9 - 9 3 = = 2 3 arctan 3 - arctan 1 = 2 3 3 - π 4 = 18

Les résultats correspondaient.

Réponse : ∫ 9 18 2 x 2 x - 9 d x = π 18

Intégration par parties lors du calcul d'une intégrale définie

Si sur le segment [a; b], les fonctions u (x) et v (x) sont définies et continues, alors leurs dérivées du premier ordre v "(x) · u (x) sont intégrables, donc à partir de cet intervalle pour la fonction intégrable u" (x ) · v ( x) l'égalité ∫ abv "(x) u (x) dx = (u (x) v (x)) ab - ∫ abu" (x) v (x) dx est vraie.

La formule peut alors être utilisée, il faut calculer l'intégrale a b f (x) d x, et ∫ f (x) d x il a fallu la rechercher par intégration par parties.

Exemple 5

Calculer l'intégrale définie ∫ - π 2 3 π 2 x · sin x 3 + π 6 d x.

Solution

La fonction x · sin x 3 + π 6 est intégrable sur l'intervalle - π 2 ; 3 2, donc c'est continu.

Soit u (x) = x, alors d (v (x)) = v "(x) dx = sin x 3 + π 6 dx, et d (u (x)) = u" (x) dx = dx, et v (x) = - 3 cos 3 + π 6. De la formule ∫ a b v "(x) u (x) d x = (u (x) v (x)) a b - ∫ a b u" (x) v (x) d x nous obtenons

∫ - π 2 3 π 2 x sin x 3 + π 6 dx = - 3 x cos x 3 + π 6 - π 2 3 π 2 - ∫ - π 2 3 π 2 - 3 cos x 3 + π 6 dx = = - 3 3 π 2 cos π 2 + π 6 - - 3 - π 2 cos - π 6 + π 6 + 9 sin x 3 + π 6 - π 2 3 π 2 = 9 π 4 - 3 π 2 + 9 sin π 2 + π 6 - sin - π 6 + π 6 = 9 4 - 3 π 2 + 9 3 2 = 3 π 4 + 9 3 2

L'exemple peut être résolu d'une autre manière.

Trouver l'ensemble des primitives de la fonction x sin x 3 + π 6 par intégration par parties en utilisant la formule de Newton-Leibniz :

∫ x sin xx 3 + π 6 dx = u = x, dv = sin x 3 + π 6 dx ⇒ du = dx, v = - 3 cos x 3 + π 6 = = - 3 cos x 3 + π 6 + 3 ∫ cos x 3 + π 6 dx = = - 3 x cos x 3 + π 6 + 9 sin x 3 + π 6 + C ⇒ ∫ - π 2 3 π 2 x sin x 3 + π 6 dx = - 3 cos x 3 + π 6 + 9 sincos x 3 + π 6 - - - 3 - π 2 cos - π 6 + π 6 + 9 sin - π 6 + π 6 = = 9 π 4 + 9 3 2 - 3 2 - 0 = 3 4 + 9 3 2

Réponse : ∫ x sin x x 3 + π 6 d x = 3 π 4 + 9 3 2

Si vous remarquez une erreur dans le texte, veuillez la sélectionner et appuyez sur Ctrl + Entrée

Une intégrale définie de la fonction continue F(X) sur le segment fini [ une, b] (où) est appelé l'incrément de certains de ses dérivés sur ce segment. (En général, la compréhension sera sensiblement plus facile si nous répétons le sujet de l'intégrale indéfinie) Dans ce cas, la notation est utilisée

Comme vous pouvez le voir dans les graphiques ci-dessous (l'incrément de la fonction primitive est indiqué), une intégrale définie peut être positive ou nombre négatif (Il est calculé comme la différence entre la valeur de la primitive à la limite supérieure et sa valeur à la limite inférieure, c'est-à-dire comme F(b) - F(une)).

Les nombres une et b sont appelés respectivement les limites inférieure et supérieure d'intégration, et le segment [ une, b] Est un segment d'intégration.

Donc si F(X) Y a-t-il une fonction primitive pour F(X), alors, selon la définition,

(38)

L'égalité (38) s'appelle par la formule de Newton-Leibniz ... Différence F(b) – F(une) s'écrivent brièvement comme suit :

Par conséquent, la formule de Newton-Leibniz s'écrira comme suit :

(39)

Montrons que l'intégrale définie ne dépend pas de la primitive de l'intégrande prise lors de son calcul. Laisser être F(X) et ( N.-É.) Sont des primitives arbitraires de l'intégrande. Puisque ce sont des primitives de la même fonction, elles diffèrent par un terme constant : Ф ( N.-É.) = F(X) + C... C'est pourquoi

Ainsi, il a été établi que sur le segment [ une, b] incréments de toutes les primitives de la fonction F(X) rencontre.

Ainsi, pour calculer une intégrale définie, il est nécessaire de trouver n'importe quelle primitive de l'intégrande, c'est-à-dire il faut d'abord trouver l'intégrale indéfinie. Constant AVEC est exclu des calculs ultérieurs. Ensuite, la formule de Newton-Leibniz est appliquée : la valeur de la borne supérieure est substituée dans la fonction primitive b , plus loin - la valeur de la limite inférieure une et la différence est calculée F (b) - F (a) . Le nombre résultant sera une intégrale définie..

À une = b par définition, il est accepté

Exemple 1.

Solution. On trouve d'abord l'intégrale indéfinie :

Application de la formule de Newton-Leibniz à la primitive

(à AVEC= 0), on obtient

Cependant, lors du calcul d'une intégrale définie, il est préférable de ne pas trouver la primitive séparément, mais d'écrire immédiatement l'intégrale sous la forme (39).

Exemple 2. Calculer l'intégrale définie

Solution. En utilisant la formule

Propriétés d'une intégrale définie

Théorème 2.La valeur de l'intégrale définie ne dépend pas de la désignation de la variable d'intégration, c'est à dire.

(40)

Laisser être F(X) Est-ce que la primitive de F(X). Pour F(t) la primitive est la même fonction F(t), dans laquelle la variable indépendante n'est notée que différemment. D'où,

Sur la base de la formule (39), la dernière égalité signifie l'égalité des intégrales

Théorème 3.Le facteur constant peut être retiré du signe d'une intégrale définie, c'est à dire.

(41)

Théorème 4.Une intégrale définie de la somme algébrique d'un nombre fini de fonctions est égale à la somme algébrique des intégrales définies de ces fonctions, c'est à dire.

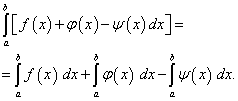(42)

Théorème 5.Si le segment d'intégration est divisé en parties, alors l'intégrale définie sur l'ensemble du segment est égale à la somme des intégrales définies sur ses parties, c'est à dire. si

(43)

Théorème 6.Lorsque les limites d'intégration sont réarrangées, la valeur absolue d'une intégrale définie ne change pas, mais seul son signe change, c'est à dire.

(44)

Théorème 7(théorème de la valeur moyenne). L'intégrale définie est égale au produit de la longueur de l'intervalle d'intégration par la valeur de l'intégrande en un point à l'intérieur de celui-ci, c'est à dire.

(45)

Théorème 8.Si la limite supérieure d'intégration est supérieure à la limite inférieure et que l'intégrande est non négative (positive), alors l'intégrale définie est également non négative (positive), c'est-à-dire si

Théorème 9.Si la limite supérieure d'intégration est supérieure à la limite inférieure et que les fonctions et sont continues, alors l'inégalité

peut être intégré terme par terme, c'est à dire.

(46)

Les propriétés d'une intégrale définie permettent de simplifier le calcul direct des intégrales.

Exemple 5. Calculer l'intégrale définie

En utilisant les théorèmes 4 et 3, et en trouvant les primitives, les intégrales tabulaires (7) et (6), on obtient

Intégrale définie avec limite supérieure variable

Laisser être F(X) est continue sur le segment [ une, b] fonction, et F(X) est sa primitive. Considérons l'intégrale définie

(47)

et après t la variable d'intégration est indiquée pour ne pas la confondre avec la borne supérieure. Quand ça change N.-É. l'intégrale définie (47) change également, c'est-à-dire c'est une fonction de la limite supérieure d'intégration N.-É., que nous désignons par F(N.-É.), c'est à dire.

(48)

Montrons que la fonction F(N.-É.) est la primitive de F(X) = F(t). En effet, différencier F(N.-É.), on a

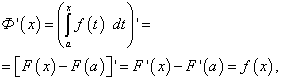
car F(X) Est-ce que la primitive de F(X), une F(une) est une valeur constante.

Fonction F(N.-É.) fait partie de l'ensemble infini de primitives pour F(X), à savoir celui qui pour X = une disparaît. Cette affirmation est obtenue si on met en égalité (48) X = une et utilisez le théorème 1 de la section précédente.