Construire des diagrammes vectoriels des courants et des tensions en fonction de la fréquence. Diagrammes vectoriels dans les circuits de courant et de tension - un guide pour la mise en place des circuits secondaires
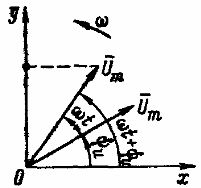
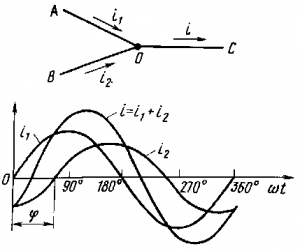
Méthode vectorielle d'affichage de quantités variant de manière sinusoïdale. Lors de l'étude des processus se produisant dans les chaînes courant alternatif, il est pratique d'utiliser la méthode de l'image vectorielle de quantités variant de manière sinusoïdale. Cette méthode est basée sur le fait que lorsqu'un certain vecteur OA tourne (Fig. 170, a) avec une vitesse angulaire uniforme ? la projection de l'OB de ce vecteur sur l'axe vertical fixe y - y est proportionnelle au sinus de l'angle ?t formé par le vecteur OA avec l'axe horizontal x - x, c'est-à-dire OB = OA sin?t. Par conséquent, la courbe exprimant la dépendance de la longueur de projection de l'OF sur l'angle θt pour un tour du vecteur OA sera une sinusoïde (Fig. 170, b). Si la valeur d'amplitude du courant alternatif Im est prise comme la longueur (module) du vecteur, alors la courbe résultante sera une représentation graphique du changement de la valeur instantanée du courant I à partir de l'angle t. A ?T = 0 (point 1) le vecteur OA sera situé horizontalement et i = 0 ; à t = 90° (point 2), le vecteur OA est situé verticalement vers le haut et i = I t ; à Δt = 180° (point 3), le vecteur OA est également situé horizontalement et i = 0 ; at?t = 270° (point 4)
le vecteur OA est situé verticalement vers le bas et i = -I т (les projections OB du vecteur OA, situées au-dessus du point 0, seront considérées comme positives, et celles situées en dessous de ce point - négatives). Les points 1 à 4 de la Fig. 170, et à différentes positions du vecteur tournant OA correspondent aux points 1-4 sur la courbe du courant i (voir Fig. 170, b). Le sens de rotation des vecteurs est classiquement pris dans le sens inverse des aiguilles d'une montre, donc les angles ?T, qui sont comptés dans le sens de rotation des vecteurs, sont considérés comme positifs, et contre ce sens - négatifs.
S'il est nécessaire d'obtenir une image vectorielle de plusieurs quantités variant de manière sinusoïdale, par exemple deux courants i 1 et i 2, tracez deux vecteurs tournants OA 1 et OA 2 (Fig. 171, a) avec des modules différents 1 t1 et 1 t2
Si au moment de l'origine la quantité changeant sinusoïdalement n'est pas nulle, mais a une certaine valeur I t sin? 1 (Fig. 171, b), alors le vecteur 1 à l'instant initial à la phase ?T = 0 fait un certain angle avec l'axe horizontal ? 1 Cet angle est appelé angle de phase initial, ou phase initiale. La différence entre les phases initiales des quantités changeant de manière sinusoïdale est appelée le déphasage ou l'angle de phase. Par exemple, sinusoïde

le courant i 1 a-t-il une phase initiale ? 1, et la sinusoïde du courant i 2 - la phase initiale ? 2 Par conséquent, les courants i 1 et i 2 sont déphasés l'un par rapport à l'autre d'un angle ? =? 1 - ? 2. Cela signifie que chaque point de la sinusoïde du courant i 1 est décalé par rapport au point correspondant de la sinusoïde du courant i 2 d'un angle . Avec une image vectorielle des courants i 1 et i 2, le déphasage entre eux est exprimé sous la forme d'un angle ? entre les vecteurs OA 1 et OA 2.
De. riz. 171, a et b, on peut voir que le vecteur OA 2 au cours de sa rotation devance le vecteur OA 1, c'est-à-dire que le courant i 2, en changeant, atteint des valeurs nulles et maximales plus tôt que le courant i 1. Par conséquent, le courant i 2 est en avance de phase sur le courant i 1 d'un angle ?. On peut également supposer que le courant i 1 est en retard sur le courant i 2 d'un angle ?. Si deux grandeurs à variation sinusoïdale, par exemple les courants i 1 et i 2, passent simultanément par des valeurs nulles et maximales, alors elles sont dites en phase. Dans ce cas, ils sont représentés par deux vecteurs coïncidant en direction (? = 0). Des vecteurs représentant des courants, des tensions et des e. etc. avec, sont indiqués par les lettres correspondantes avec un point au-dessus de la désignation, par exemple,?,?,?.
Construction de diagrammes vectoriels. Les diagrammes vectoriels sont un ensemble de vecteurs représentant des quantités variant de manière sinusoïdale agissant dans un circuit électrique donné. Ils permettent de simplifier le calcul des circuits de courant sinusoïdaux et de le rendre clair en utilisant, au lieu d'une addition ou d'une soustraction algébrique, des valeurs instantanées de courants, tensions ou e variant de manière sinusoïdale. avec addition ou soustraction de leurs vecteurs. Habituellement, lors du calcul des circuits électriques de courant alternatif, nous ne sommes pas intéressés par les valeurs instantanées des courants, tensions et e. avec, il est nécessaire de déterminer uniquement leurs valeurs effectives et leur déphasage les uns par rapport aux autres. Par conséquent, lors de la construction de diagrammes vectoriels, les vecteurs fixes sont pris en compte pour un certain moment dans le temps, qui est choisi pour que le diagramme soit visuel. Les valeurs effectives des quantités correspondantes sont prises comme modules des vecteurs. Cela ne provoque qu'une diminution de la longueur de tous les vecteurs par rapport à la longueur adoptée dans la Fig. 170 et 171, 2 fois ; pourtant les angles entre les vecteurs restent inchangés.
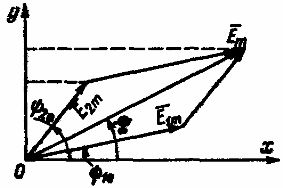
Considérons, à titre d'exemple, la construction d'un diagramme vectoriel pour les valeurs efficaces des courants i 1, i 2 et i (Fig. 172), et selon la première loi de Kirchhoff, le courant i est égal à la somme des courants i 1 et i 2. Les courants i 1 et i 2 ont des amplitudes différentes et, par conséquent, des valeurs efficaces et sont décalés l'un par rapport à l'autre d'un certain angle ?. En sommant les ordonnées des sinusoïdes i 1 et i 2, vous pouvez obtenir la courbe de courant i, en déterminer la valeur d'amplitude I t, puis la valeur efficace I = I t /? 2.
Cependant, il est plus commode de déterminer la valeur efficace du courant i en additionnant les vecteurs des courants i 1 et i 2 selon la formule

L'addition des vecteurs s'effectue selon la règle d'un parallélogramme ou d'un triangle. Dans le premier cas (Fig. 173, a), un parallélogramme ABCD est construit avec des côtés formés par des vecteurs ? 1 et ? 2. Vecteur? 1 est orienté, par exemple, horizontalement (vous pouvez dessiner ce vecteur dans n'importe quelle autre position), vector? 2 - en biais ? au vecteur ? 1 . Injection? sur le diagramme vectoriel sont comptés à partir du vecteur ? 1 dans le sens des aiguilles d'une montre, puisque pour le cas considéré le courant i 2 est en retard sur le courant i 1 d'un angle . La diagonale AC du diagramme vectoriel nous donne le vecteur total du courant résultant ?. Dans le second cas (Fig. 173, b), un triangle ABC est construit avec des côtés AB et BC égaux aux vecteurs correspondants ? 1 et ? 2 obtenir le vecteur total ? sous la forme de l'hypoténuse AC de ce triangle.
La soustraction de vecteurs de deux quantités variant de manière sinusoïdale peut être représentée comme l'addition d'un vecteur avec un autre vecteur pris avec le signe opposé. Par exemple, si les courants i et i 1 sont connus (voir figure 172), alors la valeur efficace du courant i 2 peut être obtenue en soustrayant du vecteur ? vecteur? 1, c'est-à-dire ? 2 =? -? 1 =? + (-? 1). Vecteur -? 1 a le même module que le vecteur +? 1, mais dirigé dans la direction opposée. Par conséquent, l'opération de soustraction de vecteurs? et? 1 peut être fait à l'aide de diagrammes vectoriels (Fig. 173, c et d).
Les courants de branche se trouvent immédiatement :
Pour déterminer le courant total, il est nécessaire de construire un diagramme vectoriel (Fig. 23.1, b). On commence la construction par le vecteur tension, puisqu'il est commun à toutes les branches. D'après le diagramme vectoriel, nous avons :
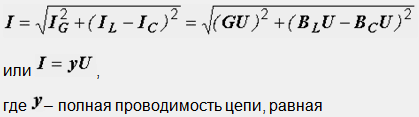
La différence entre la conductance inductive et capacitive est la conductance réactive totale du circuit B = B L -B C.

Les vecteurs des courants dans le diagramme forment un triangle de courants. Sa branche horizontale, représentant la projection du vecteur courant sur le vecteur tension, est appelée composante active du courant et est égale au courant dans l'élément actif du circuit : I a = I g = GU (Fig. 23.2, une). La projection du vecteur courant dans la direction perpendiculaire à la tension est la composante réactive du courant. Il est égal au courant total des éléments réactifs :

En divisant tous les côtés du triangle des courants par U, on obtient un triangle de conductivités (Fig.23.2, b), dont les côtés sont reliés par les relations suivantes :
2. La méthode symbolique.
Auparavant, les formules suivantes étaient obtenues :
En les substituant dans l'équation de la première loi de Kirchhoff, on obtient :

№24 Bipolaire passif dans un circuit de courant sinusoïdal. Résistance et conductivité équivalentes.
En figue. 24.1 montre un réseau passif à deux ports, composé d'éléments actifs et réactifs. Les valeurs efficaces de la tension U, du courant I et de l'angle de phase entre eux sont connues.

Construisons un diagramme vectoriel basé sur ces valeurs et, en projetant le vecteur tension sur le vecteur courant et la direction perpendiculaire à celui-ci, nous obtenons un triangle de tension formé par les côtés U a, U p, U (Fig. 24.2 a ).
Le circuit est appelé circuit équivalent séquentiel ou circuit équivalent séquentiel d'un bi-terminal passif, et ses paramètres R, X et Z sont les résistances équivalentes d'un bi-terminal.
![]()
Le triangle formé par les côtés R, X, Z et similaire au triangle de tension est le triangle de résistance
Décomposons maintenant le vecteur courant en deux composantes Ia - active, dirigée le long du vecteur tension, et réactive Ip, perpendiculaire à celui-ci (Fig. 24.3, a). Un tel diagramme vectoriel correspond à un circuit équivalent parallèle d'un dispositif à deux bornes (Fig. 24.3, b). Ses paramètres G, B et Y sont appelés conductivités équivalentes. Nous représentons les courants dans les éléments G et B comme composantes actives et réactives du courant total : Ia = GU, Ip = BU. A partir du triangle des courants (Fig. 24.3, a), on obtient un triangle des conductivités.
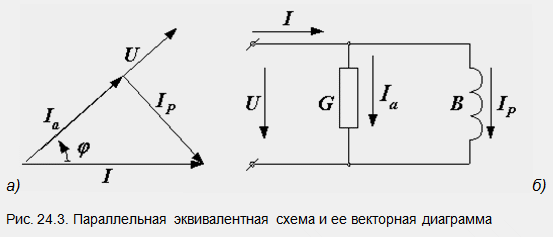
Obtenons les conditions d'équivalence des schémas ci-dessus.
Pour un circuit série U = IZ, pour un circuit parallèle I = YU, et puisque les courants et tensions dans les deux circuits sont les mêmes, alors : Y = 1 / Z et Z = 1 / Y
celles. dans tout circuit électrique, l'admittance est l'inverse de l'impédance.
Formules pour le passage d'un circuit équivalent série à un circuit parallèle :
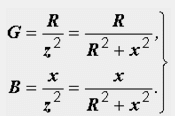
Formules pour le passage d'un circuit équivalent parallèle à un circuit séquentiel :

Veuillez noter que chacune des conductivités G et B dépend des deux résistances - active et réactive. À son tour, chacune des résistances est déterminée par les deux conductivités. Les rapports G = 1 / R et B = 1 / x ne sont valables que dans un cas particulier, le premier - à x = 0, le second - à R = 0.
Il convient de noter que les composants actifs et réactifs de la tension et du courant n'existent pas physiquement, ils ne peuvent pas être mesurés. Ils se réfèrent uniquement au schéma électrique équivalent correspondant et sont calculés. De plus, en projetant, par exemple, un vecteur de courant pour différentes tensions, nous obtenons différentes composantes pour celui-ci.
№25 Loi d'Ohm sous forme symbolique pour une chaîne arbitraire.
Que les valeurs instantanées de tension et de courant aux bornes d'un réseau passif arbitraire à deux bornes soient déterminées par des expressions dont les complexes des valeurs efficaces sont respectivement égaux:
et leur rapport détermine la résistance complexe du réseau à deux bornes :
L'inverse de la résistance complexe est la conductance complexe :
Les résistances z, R, x et les conductivités y, G et B, incluses dans les deux dernières expressions, ne sont rien de plus que les paramètres équivalents d'un réseau à deux ports.
№26 À propos du calcul des circuits de courant sinusoïdaux.
Comme il ressort du matériel théorique exposé et des exemples donnés, les diagrammes vectoriels et les nombres complexes sont largement utilisés dans l'analyse des circuits à courant sinusoïdal. En eux-mêmes, les diagrammes vectoriels sont souvent utilisés pour illustrer les résultats de la recherche théorique et de la résolution de problèmes. Ils aident à mieux comprendre l'essence des processus étudiés et à visualiser la relation et la relation des tensions et courants dans divers domaines avec les paramètres du circuit.
Dans de nombreux cas, les diagrammes vectoriels, préconstruits selon les règles ci-dessus sans aucun calcul, sont la base pour en déduire une technique spécifique pour résoudre un problème donné. Il est également possible de lier un diagramme vectoriel à des axes complexes, d'exprimer des vecteurs avec des nombres complexes et de continuer à calculer sous forme symbolique. Il n'y a pas de différence fondamentale entre la méthode du diagramme vectoriel et la méthode symbolique. Comme nous l'avons vu précédemment, derrière les opérations analytiques avec des nombres complexes, il y a certaines opérations géométriques avec des vecteurs.
Il faut également se rappeler que les vecteurs et les nombres complexes ne portent aucun contenu physique. Ce sont des abstractions purement mathématiques nécessaires à l'analyse.
La méthode symbolique est basée sur les lois d'Ohm et de Kirchhoff, qui s'écrivent sous forme symbolique de la même manière que dans les circuits à courant continu. Par conséquent, toutes les méthodes de calcul de circuits à courant continu précédemment énoncées découlant de ces lois sont également applicables pour le calcul de circuits à courant sinusoïdal sous forme symbolique.
№27 Le phénomène de résonance dans les circuits électriques.
La résonance est appelée un mode lorsque dans un circuit contenant une inductance et une capacité, le courant est en phase avec la tension. La réactance et la conductance d'entrée sont égales à zéro : x = I m Z = 0 et B = I m Y = 0. Le circuit est purement actif : Z = R ; il n'y a pas de déphasage (φ = 0).
Les tensions aux bornes de l'inductance et de la capacité dans ce mode sont de même amplitude et, étant en opposition de phase, se compensent. Toute tension appliquée au circuit tombe sur son résistance active(Fig. 27.1, a).

Les tensions d'inductance et de capacité peuvent être considérablement plus élevées que les tensions d'entrée du circuit. Leur rapport, appelé facteur Q du circuit Q, est déterminé par les valeurs des résistances inductive (ou capacitive) et active :

Le facteur de qualité montre combien de fois les tensions aux bornes de l'inductance et de la capacité à la résonance dépassent la tension appliquée au circuit. Dans les circuits d'ingénierie radio, elle peut atteindre plusieurs centaines d'unités.
De la condition ci-dessus, il s'ensuit que la résonance peut être obtenue en modifiant l'un des paramètres - fréquence, inductance, capacité. Dans ce cas, le réactif et l'impédance du circuit changent, et par conséquent, le courant, la tension sur les éléments et le déphasage. Sans donner une analyse des formules, nous montrons les dépendances graphiques de certaines de ces quantités sur la capacité (Fig. 27.2). La capacité C 0, à laquelle la résonance se produit, peut être déterminée à partir de la formule : C 0 = 1 / (ω 2 L).
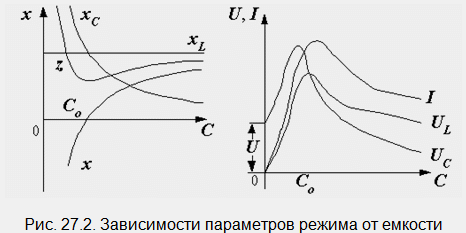
Un raisonnement similaire peut être effectué pour un circuit composé de R, L et C connectés en parallèle. Le diagramme vectoriel de son mode de résonance est illustré à la Fig. 27.1, b. Considérons maintenant un circuit plus complexe avec deux branches parallèles contenant des résistances actives et réactives (Fig. 27.3, a).
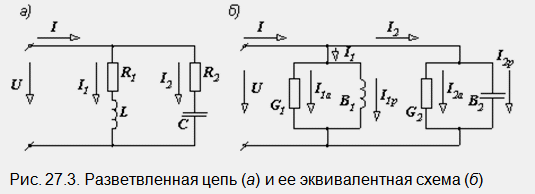
Pour elle, la condition de résonance est l'égalité à zéro de sa conductivité réactive : ImY = 0. Cette égalité signifie que l'on a la partie imaginaire expression complexe Mettez Y à zéro.
Déterminer la conductance complexe du circuit. Elle est égale à la somme des conductances complexes des branches :

En égalant à zéro l'expression entre parenthèses, on obtient :
Les côtés gauche et droit de la dernière expression ne sont rien de plus que les conductivités réactives des première et deuxième branches B1 et B2. Remplacement du circuit de la fig. 27.3, et équivalent (Fig. 27.3, b), dont les paramètres sont calculés par les formules, et en utilisant la condition de résonance (B = B1 - B2 = 0), nous arrivons à nouveau à l'expression finale.
Le schéma de la Fig. 27.3, b correspond au diagramme vectoriel représenté sur la Fig. 27,4
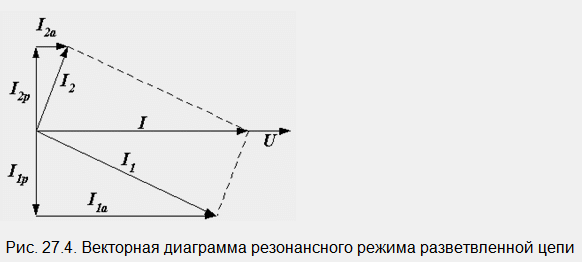
La résonance dans un circuit dérivé s'appelle la résonance des courants. Les composantes réactives des courants des branches parallèles sont opposées en phase, égales en amplitude et se compensent, et la somme des composantes actives des courants des branches donne le courant total.
№28 Énergie et puissance dans un circuit de courant sinusoïdal.
Soit une section du circuit dont la tension aux bornes est égale à vous, courant je pendant le temps dt, la charge électrique dq = idt est transférée. L'énergie dépensée par la source est égale à dw = udq = uidt, et la puissance développée p = dw / dt = ui. Cette valeur est appelée puissance instantanée et détermine la vitesse et la direction du mouvement de l'énergie dans la zone considérée. Si de l'énergie pénètre dans le circuit et s'y accumule, la fonction w (t) augmente et la puissance instantanée est positive en tant que dérivée de la fonction croissante. Tension vous et courant jeà ces moments ont les mêmes signes. Le processus d'accumulation d'énergie dans un circuit est observé, par exemple, lorsqu'un condensateur est chargé. A ces moments où vous et je ont des signes différents, la puissance instantanée est négative, la fonction w (t), qui détermine l'énergie entrant dans le circuit, diminue, puisque seule la fonction décroissante a une dérivée négative. Une perte d'énergie dans un circuit électrique signifie un retour à sa source. Cette situation se produit lorsqu'un condensateur est déchargé.
L'énergie entrant dans le circuit peut ne pas retourner à la source, mais est irréversiblement transformée en chaleur ou en travail mécanique. La quantité de cette énergie est déterminée par la loi de Joule-Lenz et pour un temps égal à la période du courant sinusoïdal est égal à :

Cette valeur, notée au temps T, détermine la valeur moyenne de la puissance instantanée sur la période et est appelée puissance active :

La puissance physiquement active est l'énergie libérée sous forme de chaleur ou de travail mécanique par unité de temps.
Que le courant et la tension à l'entrée d'un réseau passif arbitraire à deux ports soient décrits par les expressions :
En les substituant dans la formule précédente et en les intégrant, on obtient :
P = UIcos (φ)
En utilisant les rapports entre les côtés des triangles de tensions et de courants, de résistances et de conductivités, vous pouvez écrire une chaîne de formules pour calculer la puissance active :
Considérons maintenant les processus énergétiques qui se déroulent dans des éléments individuels.
En résistance active, la tension et le courant sont en phase (φ = 0); à tout moment leurs signes sont les mêmes, la puissance instantanée est positive, c'est-à-dire il reçoit constamment l'énergie d'un courant électrique, se transformant en thermique ou en mécanique. La puissance active est égale à :
Dans les éléments réactifs, l'angle de phase est égal à 90°. En inductance, avec un courant en retard, il est positif, en capacité, avec un courant en avance, il est négatif. En remplaçant φ = + - 90 ° dans l'expression de la tension à l'entrée du circuit, on obtient u = Um sin (ωt + -90 °) = + -Um cos (ωt). A cette tension, la puissance instantanée fluctue à une fréquence double, évoluant selon une loi sinusoïdale :
celles. change de signe deux fois en une demi-période. La substitution de cette expression conduit au résultat : P = 0. L'égalité de puissance active à zéro signifie qu'il n'y a pas de transformation irréversible de l'énergie électromagnétique en énergie thermique et mécanique dans les éléments réactifs.
On peut montrer que dans l'inductance pendant le premier quart de la période, lorsque le courant augmente de zéro à Im, l'énergie W M = (LI 2 m) / 2 s'accumule dans le champ magnétique de l'inductance. Au cours du prochain trimestre de la période, lorsque le courant diminue jusqu'à zéro, cette énergie de champ magnétique retourne au circuit externe.
Dans la capacité - de même : pendant un quart de la période, lorsque la tension sur les plaques du condensateur augmente de zéro à Um, le condensateur est chargé, de l'énergie s'accumule dans son champ électrique : W e = (CU 2 m) / 2. Au cours du prochain quart de la période, le condensateur est déchargé, sa tension diminue jusqu'à zéro et l'énergie accumulée dans le champ électrique est renvoyée au circuit. L'énergie que le champ électrique du condensateur et le champ magnétique de la bobine échangent avec le circuit sera appelée énergie d'échange.
Pour l'énergie du champ magnétique W M et du champ électrique W E, les formules suivantes peuvent s'écrire :

Les quantités Q L = I 2 X L et Q C = I 2 X C ayant la dimension de puissance sont appelées respectivement la puissance réactive de l'inductance et la puissance réactive du condensateur. Ils n'ont aucun rapport avec le travail effectué par le courant alternatif, mais sont des quantités proportionnelles à l'énergie des champs magnétique et électrique : Q L = ωW M, Q C = ωW E.
Dans un circuit contenant à la fois une inductance et une capacité, les fluctuations d'énergie se produisent de telle sorte qu'aux moments où le champ magnétique de l'inductance accumule de l'énergie, le champ électrique de la capacité cède de l'énergie, et vice versa. C'est-à-dire que lorsque l'énergie du champ magnétique est positive, l'énergie du champ électrique est négative. L'énergie totale des champs électrique et magnétique pour un quart de la période est égale à :
où Q est la puissance réactive du circuit, elle est proportionnelle à l'énergie totale des champs électrique et magnétique et peut être déterminée par les réactances :
A la résonance, lorsque X L = X C, les puissances réactives Q L et Q C et les énergies W M et W E accumulées dans les champs magnétique et électrique sont égales. Dans ce cas, l'échange d'énergie entre l'inductance et la capacité se produit sans la participation de la source.
Pour calculer la puissance réactive, vous pouvez écrire une chaîne de formules :
Lors de l'analyse des circuits électriques, un triangle de puissance est souvent utilisé, qui peut être obtenu en multipliant les côtés du triangle de résistance par le carré du courant (Fig. 28.1). Les relations suivantes sont valables pour elle :
La lettre S à côté de l'hypoténuse du triangle indique la puissance apparente. Il peut être calculé à l'aide de l'une des formules suivantes :
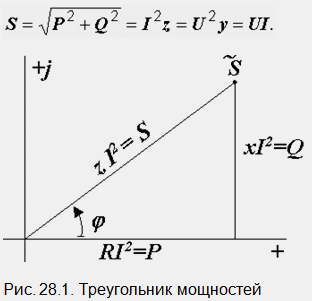
La puissance totale est déterminée par l'énergie électrique générée par le générateur et fournie au circuit. Il caractérise les dimensions des machines et appareils électriques. L'amplitude de la tension détermine le niveau d'isolation - son épaisseur et la distance entre les fréquences porteuses de courant, et le courant - la section transversale du conducteur, les conditions de refroidissement de la machine.
A cosφ = 1, la puissance apparente est égale à la valeur la plus élevée de la puissance active pouvant être obtenue pour une tension et un courant donnés.
Les unités de mesure de puissance, ayant la même dimension, sont appelées différemment. L'unité de puissance active est le watt (W), la puissance réactive est le volt-ampère réactif (var), la puissance totale est le volt-ampère (VA).
La puissance complexe est déterminée par le produit du complexe de tension et du complexe de courant conjugué :
№29 Le phénomène d'induction mutuelle.
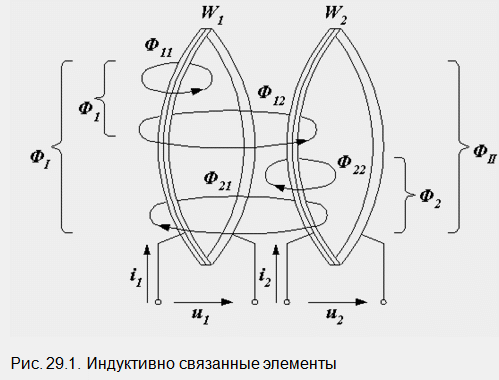
Soit deux bobines enroulées sous la forme d'anneaux minces. Leurs résistances actives sont égales à zéro, le nombre de tours est W1 et W2. Les bobines sont suffisamment proches les unes des autres, de sorte que le champ magnétique de chacune d'elles, avec une partie de sa partie, recouvre la voisine. Une image schématique des flux magnétiques créés par les courants i 1 et i 2 est montrée à la Fig. 29.1. Chaque flux est affiché comme un ligne électrique, désigné par la lettre avec deux indices. La première indique le numéro de la bobine par le courant dont elle est créée (l'origine du flux magnétique), la seconde indique le numéro de la bobine couverte par ce flux (l'objet de son influence). Considérez les flux magnétiques de la première bobine. Le courant crée un flux 1, appelé flux d'auto-induction. Sa partie Ф 11 ne couvre que la première bobine, et W E couvre également les spires de la seconde. Au total, ils sont égaux à 1. De plus, les spires de la première bobine sont couvertes par le flux 21, appelé flux d'induction mutuelle et faisant partie du flux Ф 2 créé par le courant de la deuxième bobine i 2. Le flux magnétique total Ф I, pénétrant dans la première bobine, est la somme des flux d'auto-induction 1 et d'induction mutuelle Ф 21. La somme est prise algébrique I = Ф 1 + -Ф 21, puisque ces flux peuvent être dirigés de la même manière, ou opposés les uns aux autres. L'image de la fig. 29.1 correspond au deuxième cas.
où ψ 1 = W 1 Ф 1 - propre liaison de flux de la première bobine (liaison de flux d'auto-induction); ψ 21 = W 1 Ф 21 - liaison de flux d'induction mutuelle.
Chacune de ces liaisons de flux est proportionnelle au courant qui la crée : ψ 1 = L 1 i 1 et ψ 21 = Mi 2. Par conséquent, I = L 1 i 1 + -Mi 2. Lorsque le flux magnétique change dans la bobine, la force électromotrice de l'induction électromagnétique est induite et une tension apparaît à ses bornes :

Une équation similaire peut être écrite pour la deuxième bobine.
Le premier terme à droite de la dernière équation U 1L est la tension due au courant de la bobine elle-même (tension d'auto-induction), et le second U 1M est la tension induite aux bornes de la première bobine par le changement champ magnétique de la deuxième bobine (tension d'induction mutuelle). Ces tensions ont les mêmes signes pour le sens concordant des flux magnétiques et différents pour le sens opposé.
Pour résoudre le problème de la nature de la mise sous tension des bobines et du sens de leurs flux magnétiques, la notion de bornes de même nom est introduite en les marquant sur le schéma avec les mêmes icônes. Le balisage se fait selon la définition suivante.
Les pinces du même nom de deux bobines sont de telles pinces lorsque, avec les mêmes sens de courants par rapport à ces pinces, les flux magnétiques d'auto-induction et d'induction mutuelle dans chaque bobine sont ajoutés.
En d'autres termes, si nous avons deux bobines, dans lesquelles les débuts et les fins de l'enroulement sont marqués, et si les courants y circulent de la même manière, par exemple, du début à la fin dans les deux bobines, alors les deux Flux magnétique dans chacun d'eux sera dirigé selon.
La présence d'une liaison magnétique entre les bobines est indiquée sur les schémas par une flèche arquée à double face, à côté de laquelle la lettre i 1 est placée.
№30 Connexion en série d'éléments à couplage inductif.
Soit deux bobines avec les résistances R1 et R2, les inductances L1 et L2 et l'inductance mutuelle M connectées en série (Fig. 30.1).

Il existe deux types possibles de leur connexion - la consonne et le compteur. Si nous supposons que les astérisques marquent le début des enroulements, alors avec une inclusion concordante, le début du second est connecté à la fin du premier (Fig. 30.1, a). Les courants dans les deux bobines sont dirigés de la même manière par rapport aux bornes du même nom : du début à la fin. Lorsque les bobines sont allumées en sens inverse, l'extrémité de la seconde est connectée à l'extrémité de la première (Fig. 30.1, b).
La tension sur chacune des bobines contient trois composantes : la chute de tension aux bornes de la résistance active, la tension d'auto-induction et la tension d'induction mutuelle :

Ces derniers ont les mêmes signes pour une consonne et différents pour un compteur. La tension à l'entrée du circuit est égale à la somme de ces deux tensions :
![]()
L'impédance complexe d'entrée du circuit est obtenue à partir de la considération conjointe des trois dernières équations :

où Z1 et Z2 sont les résistances complexes des bobines, et Z M est la résistance complexe d'induction mutuelle :
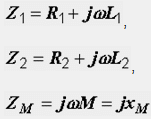
La formule ci-dessus implique les formules qui déterminent l'inductance totale du circuit et le total réactance inductive:
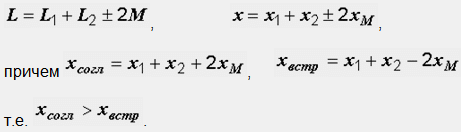
La réactance inductive résultante de chaque bobine peut être déterminée. Dans le premier, il est égal à X 1 + -X M. Et ici, avec une inclusion de consonnes, c'est plus grand qu'avec un compteur. Physiquement, cela s'explique par le fait que dans le premier cas le flux magnétique recouvrant chaque bobine est plus important que dans le second ; par exemple, pour la première bobine Ф Isogl = Ф 1 + Ф 21, et Ф Ivstr = Ф 1 -Ф 21. En conséquence, la FEM de l'induction électromagnétique, qui fournit une résistance inductive au courant, avec une connexion concordante est supérieure à celle d'un compteur.
En figue. 30.1 montre des diagrammes vectoriels construits selon les équations (30.1) et (30.2).

Avec la connexion inverse, l'effet dit "capacitif" est possible, lorsque la tension aux bornes de l'une des bobines est déphasée par rapport au courant (tension sur la figure 30.1, b). Cela se produit lorsque l'inductance de la bobine est inférieure à la valeur de l'inductance mutuelle. Dans ce cas, l'inductance résultante de la bobine considérée (en tenant compte de l'induction mutuelle) est négative : L2-M<0. Для всей цепи такой эффект невозможен. Ее индуктивность всегда положительна, и цепь носит активно-индуктивный характер.
№31 Connexion en parallèle d'éléments à couplage inductif.
Supposons que deux bobines couplées inductivement avec les paramètres R1, R2, L1, L2 et M soient connectées en parallèle (Fig. 3.5). Nous allons considérer les deux types de connexion en même temps. Une connexion concordante est obtenue lorsqu'elle est connectée au même nœud de même nom pinces, l'inverse

points. On note les équations de Kirchhoff pour le circuit considéré et on les résout, on obtient des expressions qui déterminent les courants : Le premier cas est marqué sur le schéma par des astérisques, le second

La résistance complexe d'entrée du circuit est égale au rapport tension/courant à ses bornes :
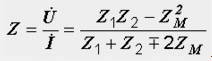
En l'absence de couplage magnétique entre les bobines, en supposant Z M = 0, on obtient la formule bien connue pour déterminer la résistance totale de deux branches parallèles :
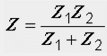
Dans toutes les expressions ci-dessus, pour les termes à double signe, le signe supérieur désigne la consonne, le signe inférieur au compteur.
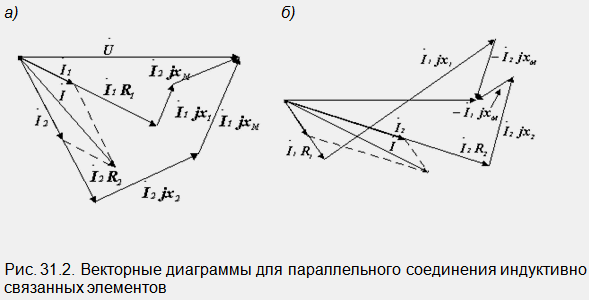
En figue. 31.2 montre des schémas vectoriels du circuit considéré avec les connexions en consonne (a) et en vis-à-vis (b) des bobines. Lors de la construction, les vecteurs I 1 jX 1 et I 1 jX M sont dessinés perpendiculairement au courant I 1, et les vecteurs I 2 jX 2 et I 2 jX M sont perpendiculaires au courant I 2. Avec une connexion concordante, les tensions d'induction mutuelle sont en avance sur les courants correspondants, avec celle venant en arrière, elles sont en retard.
№32 Marquage des bornes des bobines à couplage inductif.
Si le marquage est effectué lors de la fabrication des bobines, les pinces du même nom peuvent être indiquées en traçant le sens d'enroulement. Pour deux bobines, c'est très facile à faire (Fig. 32.1, a).
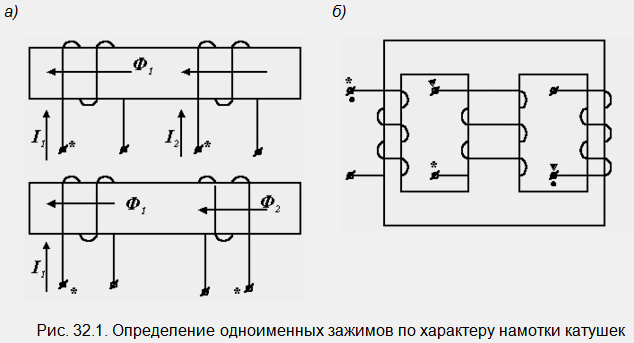
Nous procédons comme suit. Nous marquons l'une des bornes de la première bobine avec une sorte d'icône, par exemple un astérisque. Supposons que ce soit le début de l'enroulement. Nous y dirigeons le courant du début à la fin et, à l'aide de la règle de la main droite, déterminons la direction du flux magnétique: avec notre main droite, nous couvrons la bobine de sorte que quatre doigts indiquent la direction du courant dans ses tours, alors le pouce courbé montrera la direction du flux magnétique. Dans la deuxième bobine, on dirige le courant de manière à ce que son flux magnétique ait le même sens. La pince à partir de laquelle le courant circule dans la bobine est également le début. Nous le marquons également d'un astérisque.
Un cas plus complexe est illustré à la Fig. 32.1, b. Il s'avère qu'ici, il est impossible de spécifier les pinces du même nom pour les trois bobines à la fois. Nous devons les considérer par paires et agir comme nous venons de le décrire. En même temps, en considérant séparément une paire de bobines, nous ne faisons pas attention au noyau du circuit magnétique avec la troisième bobine.
Dans le cas où le sens d'enroulement des bobines est inconnu et qu'il est impossible de l'installer sans détruire la bobine, ils ont recours à des instruments de mesure électriques.
Une voie possible est la suivante. Les deux bobines sont montées alternativement dans les circuits illustrés à la Fig. 3.8, et connecté à une source de tension sinusoïdale de même amplitude.
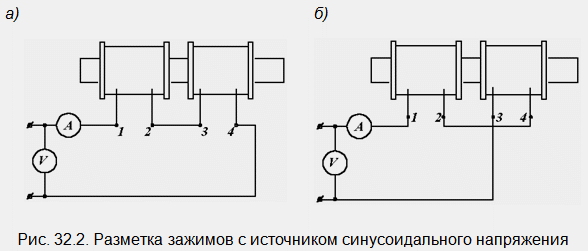
De toute évidence, dans un cas, une connexion consonne est obtenue, dans l'autre - une connexion opposée. Le type de connexion est déterminé par les lectures de l'ampèremètre. Rappelons que lorsque les bobines sont concordantes, leur impédance plus, et, par conséquent, avec la même valeur de la tension d'entrée, le courant est inférieur à celui de l'opposé. Et après avoir déterminé le type de connexion, nous faisons facilement un balisage: avec une connexion série cohérente, les bobines sont connectées les unes aux autres avec des pinces opposées (du début de la seconde à la fin de la première). Si dans la fig. 33.2 avec les mêmes relevés de voltmètre, l'ampèremètre indique 1,5 A dans le circuit gauche et 1,1 A dans le circuit droit, puis à gauche nous avons une connexion opposée, à droite une consonne, et donc la première et la quatrième, ainsi que le deuxième et troisième, sont les mêmes terminaux.
Montrons une autre façon de marquer. On connecte la première bobine par l'intermédiaire d'une clé à une source de tension constante, par exemple, à une batterie d'accumulateurs ; nous connectons le galvanomètre (ou voltmètre) du système magnétoélectrique aux bornes de la deuxième bobine (Fig. 32.3, a).

La pince de la première bobine, connectée au pôle positif de la source, est marquée d'une certaine manière, par exemple, nous y attachons une étiquette. Ensuite, nous fermons la clé. Si la flèche de l'appareil est projetée sur la balance, nous accrochons la même étiquette à la borne de la deuxième bobine, qui est connectée à la borne positive de l'appareil (borne 3). Si la flèche dévie vers la gauche, au-delà de l'échelle, alors la pince 4 du même nom avec la pince 1 est.
Aux fins de la justification théorique de la méthode, nous allons mener cette expérience avec des bobines, les directions d'enroulement et les bornes du même nom sont connues (Fig. 32.3, b).
Lorsque la clé est fermée, un courant i 1 croissant apparaît dans la première bobine, ce qui crée un flux magnétique 1, qui augmente également en amplitude. Ce dernier induit une CEM d'induction électromagnétique dans la seconde bobine. Le courant i 2 qu'il crée excite le flux magnétique 2 dont la direction est opposée à la direction de Ф 1, puisque, selon le principe de Lenz, il doit contrecarrer son augmentation. Et le flux magnétique de cette direction est créé par le courant dont la direction est indiquée sur le schéma. Nous vous rappelons que les directions du courant dans la bobine et le flux magnétique généré par celle-ci sont liés par la règle de la main droite. Le courant i 2 dans le circuit considéré circule dans le galvanomètre de sa borne positive à la borne négative. Avec cette direction du courant à travers l'appareil, sa flèche est projetée sur la balance.
Le résultat de ce raisonnement est la règle empirique suivante : si au cours de l'expérience, lorsque la clé est fermée, la flèche du dispositif du système magnétoélectrique dévie vers l'échelle, alors les pinces reliées au plus de la batterie et au plus de l'appareil portent le même nom.
№33 Circuit complexe à inductance mutuelle.
Soit un circuit à double circuit contenant des éléments couplés inductivement (Fig. 3.10). Pour le calculer, il faut établir trois (selon le nombre de courants inconnus) équations selon les lois de Kirchhoff. La première équation, pour le nœud supérieur, ne pose pas de difficultés : I1 + I2-I3 = 0

Riz. 33.1. Circuit complexe à inductance mutuelle
Nous écrirons deux autres équations selon la deuxième loi de Kirchhoff pour les contours indiqués par les flèches arrondies I et II, montrant la direction du parcours du contour lors de l'écriture des équations. Mais il faut d'abord déterminer le type d'activation des bobines. Pour chacune de leurs paires, les pinces du même nom sont marquées de leurs propres icônes. Supposons qu'il s'agisse du début des enroulements. Les première et deuxième bobines, les bornes du même nom sont marquées d'astérisques, sont incluses dans le sens opposé, car dans la première le courant circule du début à la fin et dans la seconde de la fin au début. Posons pour mémoire à côté de la flèche M 12 la lettre B (inclusion ci-contre). Dans les deuxième et troisième bobines, le début des enroulements est indiqué par des points. Dans les deux bobines, les courants circulent de la même manière par rapport à ces bornes - du début à la fin, ce qui signifie que les bobines sont allumées selon ; on met la lettre c à côté de la flèche (inclusion consonne). Nous faisons de même avec le reste des bobines.
On écrit l'équation du premier circuit :

Donnons quelques explications. La tension aux bornes d'une bobine couplée inductivement à une autre bobine est la somme de la tension d'auto-induction (IjωL) et de la tension d'induction mutuelle (IjωM). Avec une inclusion concordante, ces tensions ont les mêmes signes, avec un opposé, elles sont différentes. Pour une meilleure perception, les indices de la lettre M sont réglés de manière à indiquer la bobine qui crée le champ magnétique (premier indice) et la bobine dans laquelle la CEM est induite (deuxième indice). Par exemple, la désignation M 32 montre que nous déterminons l'influence de la troisième bobine sur la seconde. Considérez les composantes de la tension aux bornes de l'élément L 2. Dans l'équation (3.4), ils sont unis par l'accolade U L2. Le premier terme -I2jωL est la tension d'auto-induction. Il s'écrit avec un moins, car en contournant le contour, on longe cet élément à contre-courant. Le deuxième terme I1jωM 12 est la tension induite aux bornes de la deuxième bobine par le flux magnétique créé par le courant dans la première bobine. Son signe (plus) est opposé au signe de la tension d'auto-induction en raison de la connexion opposée. La tension induite dans la deuxième bobine du troisième côté (I3jωM 32) a le même signe (moins) que la tension d'auto-induction, puisque les deuxième et troisième bobines sont connectées selon.
On donne l'équation écrite pour le deuxième circuit :

№34 Remplacement équivalent des couplages inductifs.
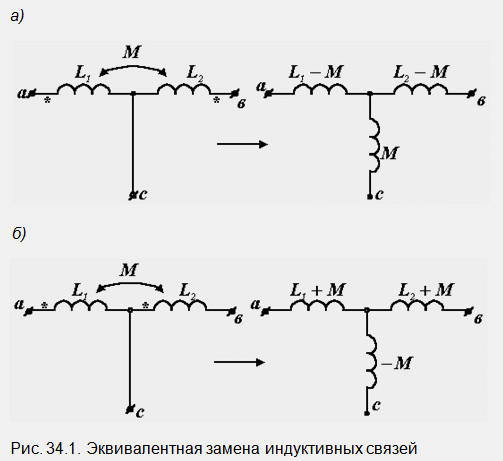
Il est possible d'éviter d'élaborer des équations aussi complexes que dans la sous-section précédente. Pour ce faire, il est nécessaire de réaliser ce que l'on appelle le découplage du circuit électrique, en remplaçant le circuit avec des éléments couplés inductivement par un circuit équivalent sans connexions inductives. Cela se fait selon la règle suivante: si deux éléments L 1 et L 2, ayant une inductance mutuelle, sont connectés au nœud du circuit électrique avec les mêmes bornes, alors dans la transition vers le circuit équivalent, -M est ajouté à ces éléments, et la branche est allumée dans la troisième branche partant du nœud M (Fig. 34.1, a).
Si la nature de la connexion des bobines change, c'est-à-dire ils sont connectés au nœud avec des bornes opposées, puis dans le circuit équivalent le signe devant M passe à l'opposé (Fig. 34.1, b).
Pour prouver les affirmations ci-dessus, il est nécessaire d'indiquer arbitrairement les directions des courants dans chaque paire de circuits (les mêmes pour la même branche) et d'écrire les expressions des tensions U ab, U bc et U ca. Pour les deux schémas, ils s'avèrent être les mêmes, ce qui confirme leur équivalence.
№35 Transformateur sans âme en acier.
Le transformateur le plus simple est une combinaison de deux enroulements placés sur un circuit magnétique commun (Fig. 35.1, a).
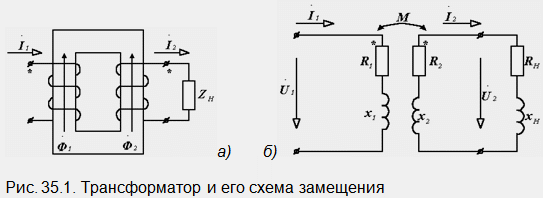
La tension de la source d'alimentation est appliquée à son enroulement primaire et la charge est connectée à l'enroulement secondaire. Les mêmes bornes des enroulements sont leurs bornes supérieures. Le courant de l'enroulement primaire I1 crée un flux magnétique F1 dans le circuit magnétique, qui à son tour dans l'enroulement secondaire provoque l'apparition du courant I2. Le flux magnétique F2 qu'il crée, conformément au principe de Lenz, empêche le flux F1, c'est-à-dire dirigé vers lui. Le sens du courant I2, correspondant au flux F2 représenté sur le schéma, est déterminé par la règle de la main droite.
Nous considérerons un transformateur qui n'a pas de noyau ferromagnétique. De tels transformateurs sont utilisés à hautes fréquences et dans des appareils de mesure électriques spéciaux. Les bobines ferromagnétiques ont des caractéristiques non linéaires et ne sont pas prises en compte ici.
Le circuit électrique équivalent du transformateur est illustré à la Fig. 35.1, b. Le schéma montre : R1, X1, R2, X2 et sont les résistances des enroulements primaire et secondaire du transformateur, R N et X H sont les résistances de charge. Nous introduisons les désignations : R22 = R2 + RH et X22 = X2 + XH - résistance active et réactive totale du circuit secondaire du transformateur, Z1 = R1 + jX1, Z2 = R2 + jX2, ZH = RH + jX H, Z22 = R22 + jX22 - résistance complexe des sections correspondantes.
Écrivons les équations de la deuxième loi de Kirchhoff pour les circuits primaire et secondaire du transformateur, en tenant compte du fait que ses enroulements ont une contre-connexion :
Notant I1jX M = E 2M, la deuxième équation du système (35.1) peut s'écrire comme suit :
E 2M = I 2 Z 2 + I 2 Z =
Physiquement, E 2M est une CEM induite dans l'enroulement secondaire par le champ magnétique alternatif de l'enroulement primaire. Dans cet esprit, l'équation peut être lue comme suit : la FEM induite dans l'enroulement secondaire du transformateur est égale à la somme des chutes de tension à travers tous les éléments de son circuit secondaire. En substituant I 2 Z H = U 2, on obtient : U 2 = E 2M -I 2 Z 2. La signification de la dernière équation est la suivante : la tension aux bornes secondaires du transformateur est inférieure à la force électromotrice induite dans l'enroulement secondaire par la quantité de chute de tension aux bornes de sa résistance.
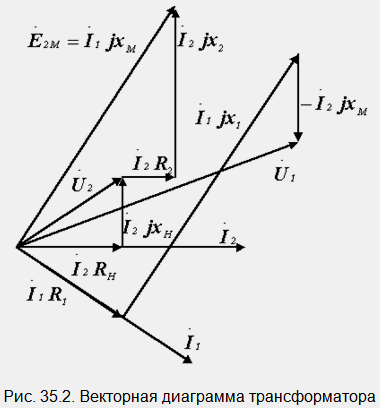
En figue. 35.2 montre un diagramme vectoriel d'un transformateur. On commence sa construction avec le courant secondaire I2. En nous concentrant sur sa direction, nous dessinons les vecteurs de tension sur tous les éléments du circuit secondaire. Leur somme est égale à EMF E 2M. Étant donné que dans la formule qui détermine sa valeur, il existe un facteur j, qui fait pivoter le vecteur d'un quart de tour, le courant est alors conduit à un angle de 90 ° par rapport à E 2M dans le sens du décalage. Après avoir déterminé la direction de I1, nous construisons les vecteurs I1R1 et I1jX1, qui avec I2jX M - donnent U1.
Divers circuits équivalents sont utilisés pour analyser le fonctionnement du transformateur. Jetons un coup d'œil à certains d'entre eux.
En connectant les deux pinces inférieures du transformateur (le mode de son fonctionnement ne changera pas) et en découplant les connexions inductives, nous arrivons au circuit équivalent en forme de T (Fig. 35.3).

A partir de la deuxième équation du système, nous exprimons le courant I2 et le substituons dans la première équation du même système :
La dernière expression correspond au circuit représenté sur la Fig. 35.3. La résistance Z BH connectée en série avec Z1 est appelée résistance d'insertion (du circuit secondaire du transformateur au primaire).
Comme il ressort de la formule, il est égal à :
Ses composants actifs et réactifs sont respectivement égaux :

L'apparition dans le circuit primaire de la résistance active introduite depuis le circuit primaire signifie physiquement ce qui suit. L'énergie fournie au transformateur est consommée non seulement par la résistance R1, mais également par les résistances du circuit secondaire R2 et R H, où elle est transmise à travers un champ magnétique alternatif entre les enroulements.
En raison du moins dans la formule de la réactance introduite, la réactance totale de l'ensemble du circuit, égale à la somme de X1 et X BH, s'avère inférieure à la réactance inductive de l'enroulement primaire.
Ceci est en bon accord avec ce qui a été dit plus tôt. Lorsque les enroulements du transformateur sont connectés en vis-à-vis, le flux Ф2, dirigé à l'opposé du flux Ф1, réduit ce dernier, ce qui entraîne une diminution de la résistance inductive totale.
№36 Système triphasé.
Un système polyphasé est un ensemble constitué de "n" circuits électriques ou circuits électriques identiques séparés, les paramètres de fonctionnement dans lesquels (e, u, i) sont décalés dans le temps d'intervalles égaux Δt = T / n ou en phase Δωt = 2π / n = 360 ° / n.
Les différentes parties du système sont appelées phases. Le terme "phase" en génie électrique a deux significations: la première - en tant que point dans le temps pour une fonction sinusoïdale de courant ou de tension, la seconde - en tant que partie d'un système polyphasé. En technologie, des systèmes à 2, 3, 6 phases et plus ont été utilisés. Dans l'industrie de l'énergie électrique, le plus répandu est le système triphasé, qui présente un certain nombre d'avantages par rapport aux systèmes avec un nombre de phases différent.
Un système triphasé est constitué de trois circuits électriques ou circuits électriques (phases), dont les paramètres de mode (u, i) sont décalés dans le temps de Δωt = 2π / 3 = 360 ° / 3 = 120 °. Les phases individuelles d'un système triphasé selon GOST sont désignées (appelées) par les lettres latines majuscules A, B, C (désignation de base), ou par les numéros 1, 2, 3 (désignation acceptable), ou les lettres latines majuscules R, S, T (appellation internationale).

Peu importe laquelle des trois phases est nommée par quelle lettre A, B ou C, leur ordre de succession dans le temps est essentiel. L'ordre direct des phases est appelé A → B → C → A, dans lequel les paramètres du mode (u, i) en phase B sont en retard de 120 ° sur ceux de la phase A et en avance de 120 ° dans la phase C °. Dans l'ordre inverse des phases A → C → B → A, les paramètres de mode de la phase C sont en retard de 120 ° sur ceux de la phase A et en avance de 120 ° dans la phase B.
Si les phases individuelles du système fonctionnent de manière isolée et indépendamment les unes des autres, le système est alors appelé non connecté. Considérez le fonctionnement du système triphasé non connecté le plus simple (Fig. 36.1). Les valeurs instantanées de la phase EMF du générateur sont décalées dans le temps de 120° dans l'ordre des phases A → B → C → A :
e A = E m sinωt ↔ E A = Ee j0 °
e B = E m sin (ωt-120°) ↔ E B = Ee -j120°
e C = E m sin (ωt-240°) = E m sin (ωt + 120°) ↔ E C = Ee j120°
Les diagrammes graphiques de ces fonctions sont illustrés à la Fig. 36.2, et vecteur - dans la Fig. 36.3.


La propriété principale de toutes les fonctions variables (e, u, i) dans un système triphasé symétrique est que la somme de leurs valeurs instantanées à tout moment est nulle, par exemple, e A + e B + e C = 0 Trouvons cette somme pour différents points dans le temps :
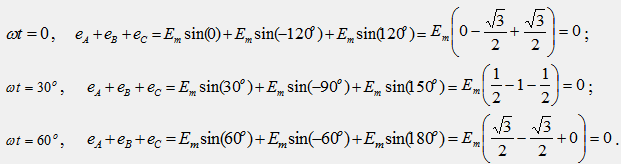
Si la charge des différentes phases est égale, c'est-à-dire ZA = ZB = ZC = Ze jφ, alors les courants de phase seront égaux en amplitude et déphasés par rapport à leur EMF (tensions) du même angle , et l'un par rapport à l'autre, comme l'EMF, sera déphasé de 120 °. Par conséquent, les courants de phase i , i В, i С forment un système triphasé symétrique et pour eux les conclusions précédemment obtenues seront valables : i А + i В + i С = 0 ; I A + I B + I C = 0.
Nous transformons un système triphasé non connecté en un système connecté en combinant trois entraînements inversés en un seul entraînement commun. Selon la 1ère loi de Kirchhoff, le courant total i N = i A + i B + i C = 0 doit circuler dans le fil commun. Cela signifie qu'il n'y a aucun besoin de fil de retour, ce qui permet d'importantes économies de les fils sont obtenus lors du transfert d'énergie d'un générateur triphasé au récepteur.
Avantages (avantages) d'un système triphasé :
1) La transmission d'énergie du générateur aux consommateurs par courant triphasé est la plus rentable économiquement qu'avec tout autre nombre de phases. Par exemple, par rapport à un système à deux fils, les économies de fils sont réalisées de moitié (3 fils au lieu de 6), respectivement, les pertes d'énergie dans les fils de ligne sont réduites.
2) Le système triphasé permet techniquement d'obtenir un champ tournant circulaire, qui sous-tend le fonctionnement de toutes les machines triphasées (générateurs et moteurs).
3) Les éléments d'un système triphasé (générateurs, transformateurs, moteurs) sont de conception simple, de fonctionnement fiable, ont un bon poids et de bonnes dimensions, sont relativement bon marché et durables.
4) À la sortie des générateurs triphasés, il existe deux niveaux de tension de sortie - linéaire et phase, différant de √3 fois (Ul / Uf = √3), ce qui vous permet de connecter des récepteurs avec des tensions nominales différentes à un tel générateur .
En raison de ses avantages, le système triphasé est utilisé dans l'industrie de l'énergie électrique pour la production, le transport, la distribution et la consommation d'énergie électrique.
Le système triphasé et ses principales liaisons - générateur, transformateur, ligne électrique, moteur - ont été développés en 1889 par l'ingénieur Dolivo-Dobrovolsky (Siemens et Schuckert). La création de ce système a été un événement important dans l'histoire du développement de l'électrotechnique théorique et appliquée.
№37 Manières de connecter les enroulements des générateurs triphasés.
Dans les enroulements d'un générateur triphasé, des champs électromagnétiques sinusoïdaux sont induits, déphasés de 120 ° :
e A = E m sinωt ↔ E A = E f e j0 °
e B = E m sin (ωt-120°) ↔ E B = E f e -j120°
e C = E m sin (ωt-240°) = E m sin (ωt + 120°) ↔ E C = E f e j120°
Les enroulements de phase du générateur peuvent être connectés entre eux de deux manières différentes : une étoile (y) et un triangle (Δ).
Lorsqu'elles sont connectées à une étoile, les extrémités des enroulements de phase (phases) du générateur sont connectées à un point commun N, appelé zéro ou neutre, et le début des enroulements sert de bornes linéaires du générateur A, B, C (fig. 37.1).
Le diagramme vectoriel des tensions d'un générateur triphasé lors de la connexion de ses enroulements de phase à une étoile est illustré à la Fig. 37.2 a, b.
Dans un générateur triphasé, les tensions de phase et de ligne sont distinguées. Les tensions de phase sont appelées tensions entre les débuts et les extrémités des enroulements de phase ou entre l'une des bornes linéaires A, B, C et la borne zéro N. Les tensions de phase sont égales à la phase EMF : UA = EA, UB = EB, UC = EC (l'indice N aux tensions de phase est abaissé, puisque φ N = 0). Les tensions linéaires sont appelées tensions entre deux bornes de ligne A, B, C. Les tensions linéaires sont égales à la différence vectorielle de deux tensions de phase : U AB = U A - U B ; UBC = U B - U C ; U CA = U C - U A.

Lors du calcul des circuits triphasés par la méthode complexe, les tensions de phase et de ligne du générateur sont présentées sous une forme complexe, avec l'un des vecteurs du système pris comme initial et aligné avec l'axe réel, et les vecteurs restants reçoivent les phases initiales selon leurs angles de décalage par rapport au vecteur initial. En figue. 37.2 a montre une variante de représentation des tensions d'un générateur triphasé sous une forme complexe, lorsque la tension de phase de la phase A est prise comme vecteur initial. Dans ce cas, les tensions de phase du générateur sous une forme complexe obtiendront la forme : UA = U fe j0 °, UB = U fe -j120 ° , UC = U fe j120 °, tensions de ligne : U AB = U le j30 °, U BC = U le -j90 °, U CA = U le j150°.
En figue. 37.2 b montre une autre variante de représentation des tensions d'un générateur triphasé sous forme complexe, lorsque la tension de ligne U AB est prise comme vecteur initial. Dans ce cas, les tensions de phase du générateur sous forme complexe obtiendront la forme suivante : UA = U fe -j30°, UB = U fe -j150°, UC = U fe j90°, tensions de ligne : U AB = U le j0°, U BC = U l e -j120°, U CA = U l e j120°.
A partir de la géométrie on obtient le rapport entre les modules de tensions linéaires et de phases : U L = 2U F cos 30° = 2UF (3) / 2 = √ (3) UF.
Les enroulements d'un générateur triphasé peuvent théoriquement être allumés selon le schéma triangulaire. Dans un tel schéma, la fin de chaque phase précédente est connectée au début de la suivante et les points de connexion servent de sorties linéaires du générateur (Fig. 37.3).
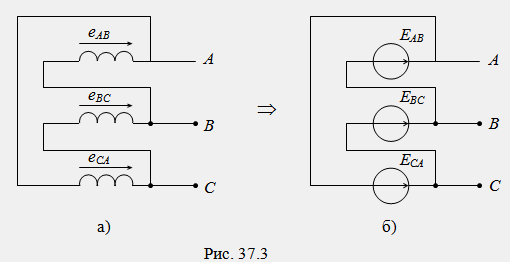
Lorsque les phases sont connectées en triangle, la somme de la phase EMF agit dans son circuit : e = e AB + e BC + e CA. Dans de vrais générateurs triphasés, il est techniquement impossible d'assurer l'égalité à zéro pour la CEM totale. Étant donné que les résistances intrinsèques des enroulements du générateur sont faibles, même une FEM totale insignifiante e> 0 peut provoquer un courant d'égalisation dans le circuit triangulaire, proportionnel au courant nominal du générateur, ce qui entraînerait des pertes d'énergie supplémentaires et une diminution de l'efficacité du générateur. Pour cette raison, les enroulements des générateurs triphasés ne doivent pas être connectés en triangle.
La tension nominale dans un système triphasé est appelée tension de ligne. La tension nominale est généralement exprimée en kilovolts (kV). L'échelle des tensions triphasées assignées utilisée en pratique est la suivante : 0,4 ; 1.1 ; 3.5 ; 6.3 ; 10,5 ; 22 ; 35 ; 63 ; 110 ; 220 ; 330 ; 500 ; 750. Au niveau du consommateur, la tension triphasée assignée peut être indiquée sous la forme d'un rapport U L ⁄U F, par exemple : U L / U F = 380 220 V.
№

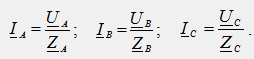
I N = I A + I B + I C
I A + I B + I C = 0


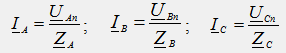

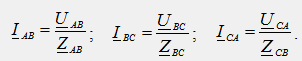

№38 Manières de connecter les phases des récepteurs triphasés.
Les récepteurs de courant triphasé peuvent être connectés au générateur de deux manières - étoile (y) et triangle (Δ). Comme vous le savez, à la sortie d'un générateur triphasé, on obtient deux tensions (linéaire et phase), différant par Ul / Uf = √3 fois. D'autre part, chaque récepteur d'énergie est conçu pour fonctionner à une certaine tension, que l'on appelle nominale. Le schéma de connexion des phases du récepteur doit garantir que ses phases sont connectées à la tension de phase nominale. Ainsi, le choix d'un schéma de connexion de phase de récepteur triphasé dépend du rapport de la tension nominale du récepteur et du générateur (réseau).
Un circuit en étoile est utilisé si la tension nominale du récepteur correspond (est) à la tension de phase du générateur. Lorsqu'il est connecté à une étoile, les extrémités des phases du récepteur sont combinées en un seul point "n", appelé zéro ou neutre, et le début des phases est connecté aux bornes linéaires du générateur triphasé A, B, C avec fils linéaires. Si le point zéro du récepteur "n" est connecté au point zéro du générateur "N" par un fil neutre, alors le circuit est appelé une étoile avec un fil neutre (Fig. 38.1a). Avec absence fil neutre le circuit s'appelle une étoile sans fil neutre (Fig. 38.1b).
Les courants circulant dans les fils linéaires du générateur au récepteur sont appelés courants linéaires.
Les courants circulant dans les phases du récepteur du début à la fin sont appelés courants de phase. Dans le circuit en étoile, les phases du récepteur sont connectées en série avec les fils de ligne et les mêmes courants (I A, I B, I C) les traversent. Ainsi, pour un circuit en étoile, les notions de courants linéaires et de phases sont identiques : I L = I F.
Le courant circulant dans le fil neutre du récepteur au générateur est appelé zéro ou neutre (I N).

Les tensions entre les débuts et les fins des phases du récepteur sont appelées phase (U An, U Bn, U Cn), et les tensions entre les débuts des phases sont dites linéaires (U AB, U BC, U CA). Les tensions de ligne du récepteur et du générateur sont identiques.
Dans un circuit en étoile avec un fil neutre (Fig.38.1a), la tension de phase du générateur est appliquée directement à chaque phase du récepteur (U AN = U An = UA, U BN = U Bn = UB, U CN = U Cn = UC), chacune des phases dans ce cas, elle fonctionne indépendamment les unes des autres et les courants linéaires (de phase) sont déterminés selon la loi d'Ohm :
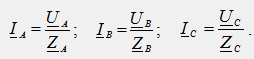
Le courant dans le fil neutre selon la première loi de Kirchhoff est égal à la somme géométrique des courants linéaires (de phase):
I N = I A + I B + I C
Avec une charge symétrique Z A = Z B = Z C, le courant dans le fil neutre I N = 0 et, par conséquent, il n'y en a pas besoin. Les récepteurs triphasés symétriques (par exemple, les moteurs électriques triphasés) sont connectés en étoile sans fil neutre.
Avec une charge déséquilibrée, la valeur relative du courant dans le fil neutre dépend de la nature et du degré d'asymétrie des courants de phase. En règle générale, les récepteurs triphasés ont tendance à être conçus de manière aussi symétrique que possible. Par conséquent, le courant dans le fil neutre dans des conditions réelles est bien inférieur aux courants linéaires (de phase).
un circuit en étoile sans fil neutre (Fig.38.1b) pour toute charge de phase, la condition de la première loi de Kirchhoff doit être satisfaite :
I A + I B + I C = 0
Il résulte de l'équation qu'une modification de l'un des courants entraîne une modification des deux autres courants, c'est-à-dire que les phases individuelles fonctionnent en mode dépendant. Avec une charge déséquilibrée, le potentiel du point zéro du récepteur Un devient non nul, il « se décale » sur le plan complexe à partir de la position zéro, tandis que les tensions de phase du récepteur (U An, U Bn, U Cn) ne sont pas égal aux tensions de phase correspondantes du générateur (UA, UB, UC), le soi-disant déséquilibre des tensions de phase du récepteur se produit (Fig. 38.2).

Le calcul des courants et des tensions dans un circuit en étoile sans fil neutre est effectué dans la séquence suivante.
La tension (potentiel) du point neutre du récepteur est déterminée par la méthode des deux nœuds :

où Z N est la résistance complexe du fil neutre, en son absence Z N = ∞.
Les tensions de phase du récepteur sont déterminées comme la différence de potentiel des points correspondants :
U An = U A -U n, U Bn = U B -U n, U Cn = U C -U n.
Les courants de phase du récepteur sont déterminés selon la loi d'Ohm :
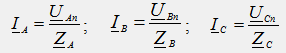
Les puissances complexes des phases du récepteur :

Le mode de fonctionnement du récepteur avec déséquilibre de tension de phase est anormal et peut entraîner une panne. Pour cette raison, une charge triphasée asymétrique ne doit pas être allumée dans un circuit en étoile sans fil neutre (par exemple, une charge d'éclairage).
Le circuit delta est utilisé si la tension de phase nominale du récepteur correspond (est) à la tension de ligne du générateur. Lorsqu'elles sont connectées en triangle, la fin de chaque phase est connectée au début de la suivante et les points de connexion (les sommets du triangle) sont connectés aux bornes linéaires du générateur triphasé A, B, C avec fils linéaires (Fig. 38.3).
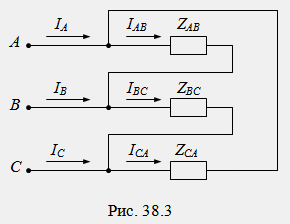
Les courants circulant dans les phases du récepteur dans le sens de leurs débuts à leurs extrémités sont appelés courants de phase (I AB, I BC, I CA). Les courants circulant dans les fils linéaires dans la direction du générateur au récepteur sont appelés linéaires (I A, I B, I C).

Dans le circuit triangulaire, les tensions de phase et de ligne du récepteur sont identiques (U AB, U BC, U CA). Dans ce schéma, chaque phase du récepteur est directement connectée à la tension de ligne du générateur, tandis que les phases individuelles fonctionnent indépendamment les unes des autres. Les courants de phase sont déterminés par la loi d'Ohm :
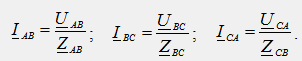
Les courants linéaires sont déterminés à partir des équations de la première loi de Kirchhoff pour les sommets du triangle, ils sont égaux à la différence géométrique entre les courants de phase :
I A = I AB -I CA; I B = I BC -I AB; I C = I CA -I BC.
En mode symétrique, les courants phase et ligne sont symétriques, tandis que le rapport de leurs modules est IL / IF = √3.
Avec une charge déséquilibrée, la relation entre les courants linéaires et de phase est déterminée par les équations de la première loi de Kirchhoff. En figue. 38.4 montre un diagramme vectoriel des courants et des tensions pour un circuit triphasé arbitraire lorsque les phases sont connectées en triangle.

№39 Calcul de circuits triphasés complexes.
Un circuit triphasé complexe, par exemple un système d'alimentation interconnecté, peut contenir un grand nombre de générateurs triphasés, de lignes électriques et de récepteurs d'énergie triphasés. Le schéma électrique d'un tel circuit est un exemple typique d'un circuit alternatif complexe. Le régime établi dans un tel schéma peut être décrit par un système d'équations algébriques à coefficients complexes, compilées selon l'une des méthodes de calcul des circuits complexes (la méthode des lois de Kirchhoff, la méthode des courants de boucle, la méthode des potentiels nodaux) . La méthode la plus rationnelle pour calculer de tels circuits triphasés est la méthode des potentiels nodaux, tandis que la formulation des équations et leur solution sont réalisées sous forme matricielle.
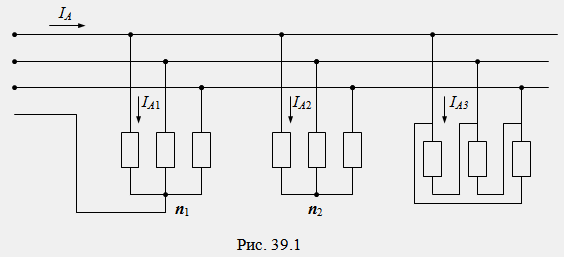
Dans des cas plus simples, il est possible d'utiliser toutes les méthodes de calcul permettant d'obtenir une solution économique au problème. En figue. 39.1 montre un schéma de la connexion en parallèle de plusieurs récepteurs triphasés avec différents schémas de connexion de phase à un générateur. Dans le schéma présenté, le calcul des courants de phase et de ligne de chacun des récepteurs peut être effectué individuellement et indépendamment les uns des autres, et les courants de ligne de la source sont déterminés comme les sommes géométriques des courants de tous les récepteurs, par exemple , IA = I A1 + I A2 + I A3.
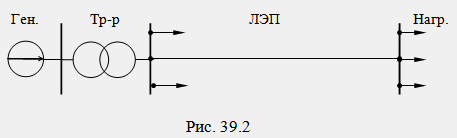
Comme vous le savez, le système électrique combiné triphasé fonctionne dans un mode proche de la symétrie. En mode symétrique, les courants et tensions des phases adjacentes ne diffèrent que par l'angle de décalage de ± 120º. Le calcul des courants et des tensions en régime permanent symétrique n'est effectué que pour l'une des phases, par exemple pour la phase A, tandis que les circuits triphasés sont représentés par des circuits équivalents monophasés. En figue. 39.2 montre un schéma symbolique de la transmission d'énergie d'un générateur triphasé à des récepteurs distants, et sur la Fig. 39.3 - circuit monophasé calculé pour le même circuit. Dans le schéma de conception de la Fig. 39.3 chaque lien de transmission de puissance correspond à son circuit équivalent standard.

À la suite de calculs, les courants et les tensions sont déterminés dans tous les éléments de circuit pour la phase A, par exemple, I A = Ie jα. Des courants et des tensions similaires dans la phase B sont déterminés en multipliant les valeurs correspondantes de la phase A par le facteur de rotation e -j120°, et pour la phase C - par le facteur e j120°.
№40 Puissance d'un circuit triphasé et méthodes de sa mesure.
Actif et puissance réactive un circuit triphasé, comme pour tout circuit complexe, sont égaux aux sommes des puissances correspondantes des phases individuelles :
où I A, U A, I B, U B, I C, U C - valeurs de phase des courants et des tensions.
En mode symétrique, les puissances des phases individuelles sont égales et la puissance de l'ensemble du circuit peut être obtenue en multipliant les puissances des phases par le nombre de phases :

Dans les expressions obtenues, nous remplaçons les quantités de phase par des linéaires. Pour le schéma en étoile, les rapports Uph / Ul / √3, I ph = I l sont vrais, alors on obtient :
Pour le circuit triangulaire, les relations suivantes sont vraies : Uf = Ul ; Si = Il / √3, alors on obtient :
Ainsi, quel que soit le schéma de raccordement (étoile ou triangle) pour un circuit triphasé symétrique, les formules de puissances ont la même forme :

Dans les formules ci-dessus pour les puissances d'un circuit triphasé, les valeurs linéaires des quantités U et I sont supposées, mais les indices ne sont pas mis dans leurs désignations.
La puissance active dans un circuit électrique est mesurée par un appareil appelé wattmètre, dont les lectures sont déterminées par la formule :
où U w, I w - vecteurs de tension et de courant fournis aux enroulements de l'appareil.

Pour mesurer la puissance active de l'ensemble du circuit triphasé, en fonction du schéma de connexion des phases de la charge et de sa nature, différents schémas de mise sous tension des instruments de mesure sont utilisés.
Pour mesurer la puissance active d'un circuit triphasé symétrique, un circuit avec un wattmètre est utilisé, qui est connecté à l'une des phases et mesure la puissance active de cette seule phase (Fig. 40.1). La puissance active de l'ensemble du circuit est obtenue en multipliant la lecture du wattmètre par le nombre de phases : P = 3W = 3U f I f cos (φ). Le circuit de wattmètre unique ne peut être utilisé que pour une estimation de puissance orientée et ne s'applique pas aux mesures de précision et commerciales.
Pour mesurer la puissance active en quatre fils circuits triphasés(en présence d'un fil neutre), un circuit à trois appareils est utilisé (Fig.40.2), dans lequel la puissance active de chaque phase est mesurée séparément et la puissance de l'ensemble du circuit est déterminée comme la somme des lectures de trois wattmètres :
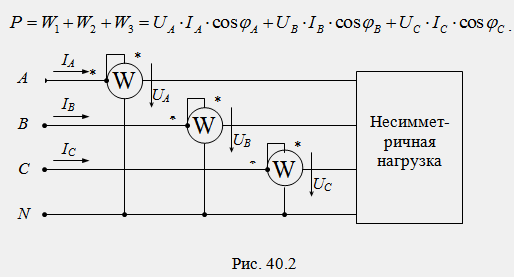
Pour mesurer la puissance active dans les circuits triphasés à trois fils (en l'absence de fil neutre), un circuit à deux appareils est utilisé (Fig. 40.3).
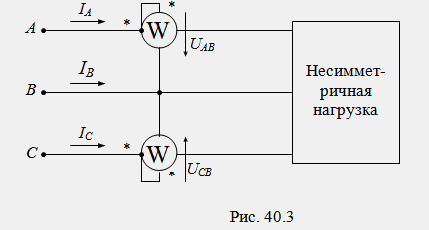
En l'absence de fil neutre, les courants linéaires (de phase) sont interconnectés par l'équation de la 1ère loi de Kirchhoff : I A + I B + I C = 0. La somme des lectures de deux wattmètres est égale à :
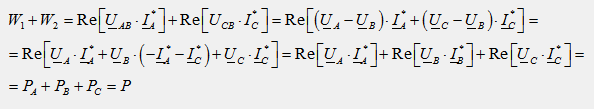

Ainsi, la somme des lectures de deux wattmètres est égale à la puissance triphasée active, tandis que la lecture de chaque appareil séparément dépend non seulement de l'amplitude de la charge, mais également de sa nature.
En figue. 40.4 montre un diagramme vectoriel des courants et des tensions pour une charge équilibrée. Il résulte du diagramme que les lectures des wattmètres individuels peuvent être déterminées par les formules :

L'analyse des expressions obtenues nous permet de tirer les conclusions suivantes. Avec une charge active (φ = 0), les lectures des wattmètres sont égales (W1 = W2).
Avec charge inductive active (0 ≤ φ ≤ 90 °), la lecture du premier wattmètre est inférieure à la seconde (W1< W2), а при φ>La lecture à 60° du premier wattmètre devient négative (W1<0).
Avec une charge capacitive active (0 φ≥ -90 °), la lecture du deuxième wattmètre est inférieure au premier (W1 est supérieur à W2), et à φ (moins) -60 °, la lecture de le deuxième wattmètre devient négatif.
№41 Champ magnétique tournant.
L'un des avantages les plus importants d'un système triphasé est la possibilité d'obtenir avec son aide un champ magnétique rotatif circulaire, qui sous-tend le fonctionnement des machines triphasées (générateurs et moteurs).
Pour obtenir un champ magnétique tournant circulaire, il est nécessaire et suffisant de remplir deux conditions. Première condition : il faut disposer 3p bobines identiques (p = 1, 2, 3,….) dans l'espace pour que leurs axes soient situés dans un même plan et soient décalés entre eux d'angles égaux = 360 °/3p. Condition deux : il faut faire passer dans les bobines des courants alternatifs égaux en amplitude et décalés dans le temps de t = T/3 ou ∆ωt = 360 °/3 = 120 ° (courant triphasé symétrique). Dans ces conditions, un champ magnétique tournant circulaire d'amplitude constante d'induction B max le long de son axe et de vitesse angulaire de rotation ωп constante sera créé dans l'espace autour des bobines.
En figue. 41.1 montre la disposition spatiale de trois (p = 1) bobines identiques à angles égaux de 120° selon la première condition.
Un courant triphasé symétrique circule dans les bobines, dans le sens de leurs origines (A, B, C) aux extrémités (X, Y, Z) :
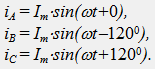
Le champ magnétique créé par chaque bobine séparément est proportionnel au courant de la bobine (B = k * i), par conséquent, les champs magnétiques des bobines individuelles au centre des coordonnées forment un système triphasé symétrique B (t):
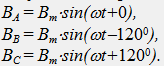

Les directions positives des champs magnétiques de chaque bobine (vecteurs B A, B B, B C) dans l'espace sont déterminées par la règle de la vis de droite selon les directions positives acceptées des courants de bobine (Fig. 41.1).
Le vecteur résultant de l'induction du champ magnétique B pour n'importe quel moment du temps peut être trouvé par addition spatiale des vecteurs B A, B B, B C de bobines individuelles. Déterminons la valeur du vecteur résultant de l'induction de champ magnétique B pour plusieurs instants de temps ωt = 0° ; 30° ; 60°. L'addition spatiale des vecteurs sera effectuée graphiquement (Fig. 41.2a, b, c). Les résultats des calculs sont résumés dans un tableau séparé :
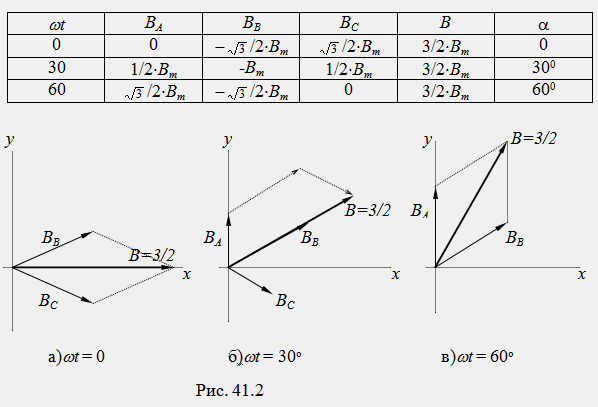
L'analyse du tableau montre que le vecteur résultant de l'induction de champ magnétique B (t, x, y) a une amplitude constante (B max = 3 / 2B m) et tourne uniformément dans l'espace dans le sens positif en direction de la bobine A vers la bobine B avec une vitesse angulaire ωп, égale à la fréquence angulaire du courant . Dans le cas général, la vitesse angulaire de rotation du champ magnétique dépend aussi du nombre de bobines :
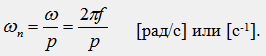
En technologie, pour caractériser la rotation d'un champ magnétique, la notion de fréquence de rotation est utilisée : n = 60f/p [rpm]
Avec un changement du nombre p, l'image spatiale du champ magnétique change : pour p = 1, le champ magnétique a deux pôles (ou une paire de pôles), pour p = 2, quatre pôles (ou 2 paires de pôles) , etc. (fig.41.3). Pour cette raison, le nombre p = 1, 2, 3, ... est appelé le nombre de paires de pôles du champ magnétique.
La fréquence de rotation du champ magnétique peut être modifiée en douceur en modifiant la fréquence du courant d'alimentation f et pas à pas - en modifiant le nombre de paires de pôles p. Dans des conditions industrielles, les deux méthodes de contrôle de la fréquence de rotation du champ sont techniquement et économiquement inefficaces. A fréquence constante du courant industriel f = 50 Hz, l'échelle des fréquences de rotation synchrone du champ magnétique en fonction du nombre de paires de pôles est la suivante :

Pour changer le sens de rotation du champ magnétique, il suffit de changer l'ordre des phases du courant d'alimentation, ou, simplement, d'intervertir deux phases quelconques de la source entre elles.
№42 Fondements théoriques de la méthode des composantes symétriques.
La méthode des composants symétriques est utilisée pour calculer les circuits triphasés en modes déséquilibrés. Les modes asymétriques dans le système d'alimentation se produisent avec divers types de courts-circuits. Le calcul des courants de court-circuit est un problème d'ingénierie important dans l'industrie de l'énergie électrique, qui est résolu par la méthode des composants symétriques.
Mathématiquement, tout système triphasé asymétrique de grandeurs vectorielles (tensions, courants, etc.) peut être représenté comme une somme (remplacée par une somme) de trois systèmes triphasés symétriques, à savoir : a) les systèmes à séquence directe avec ordre de phase direct A → B → C → A ; b) systèmes à séquence inverse avec ordre inverse des phases A → C → B → A ; c) un système homopolaire, qui se compose de trois vecteurs égaux qui coïncident en phase. Les systèmes symétriques séparés de vecteurs, dans lesquels un système asymétrique est décomposé, sont appelés composants symétriques. Les vecteurs de composantes symétriques sont indexés par des nombres : 1 - pour séquence positive, 2 - pour séquence négative et 0 - pour séquence zéro.
En figue. 42.1 présente les composants symétriques d'un certain système de tension triphasé asymétrique U A, U B, U C.
Dans la méthode des composantes symétriques, pour simplifier la forme d'écriture des équations, le coefficient a = e j120° (facteur de rotation) est utilisé, multipliant par lequel le vecteur est tourné d'un angle de 120° sans changer son module. Propriétés du facteur de rotation : a 2 = e j240° = e -j120°, a 3 = 1, a 4 = a, 1 + a + a 2 = 0.


Les vecteurs du système asymétrique d'origine sont déterminés par le principe de superposition en tant que sommes géométriques des vecteurs correspondants des composantes symétriques :
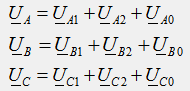
L'addition géométrique des vecteurs de composantes symétriques selon ces équations est illustrée à la Fig. 42.2.
En utilisant le facteur de rotation « a » et « a 2 », nous exprimons tous les termes du membre de droite des équations en termes de composantes symétriques de la phase A :
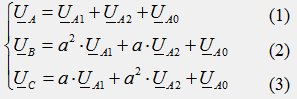
Nous multiplions tous les termes de l'équation (2) par "a", et tous les termes de l'équation (3) par "a 2", additionnons les trois équations terme par terme et obtenons :
De l'équation résultante suit la formule pour séparer la composante symétrique de la séquence positive du système asymétrique de vecteurs :

Nous multiplions tous les termes de l'équation (2) par "a 2", et tous les termes de l'équation (3) par "a", additionnons les trois équations terme par terme et obtenons :
De l'équation résultante suit la formule pour séparer la composante symétrique de la séquence négative du système asymétrique de vecteurs :

Ajoutons les trois équations (1), (2) et (3) terme par terme et obtenons :
De l'équation résultante suit la formule pour séparer la composante symétrique de la séquence zéro du système vectoriel asymétrique :

Les formules obtenues sont utilisées en pratique pour décomposer des systèmes triphasés asymétriques de vecteurs en composantes symétriques.
№43 Calcul du mode d'une charge triphasée symétrique avec une tension déséquilibrée.
Soit un système asymétrique de tensions U A, U B, U C appliqué à un récepteur triphasé symétrique, par exemple un moteur électrique. Pour obtenir des schémas généraux, nous introduisons un fil zéro avec une résistance Z N dans le circuit. Le schéma électrique prendra la forme (Fig.43.1) :
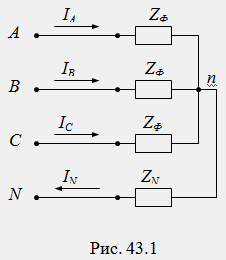
Décomposons le système asymétrique de tensions U A, U B, U C en composantes symétriques des séquences directe, inverse et nulle :
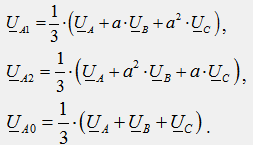
Nous appliquons la méthode de superposition au calcul du circuit et calculons les courants séparément pour chaque composante de tension symétrique. Étant donné que pour chacun des composants symétriques, le circuit générateur-récepteur triphasé est complètement symétrique, le calcul du mode ne peut être effectué que pour une phase A, respectivement, le circuit triphasé doit être remplacé par trois circuits monophasés séparément pour chaque composant (Fig. 43.2a, b, c ). En mode symétrique pour les séquences directes et inverses, le courant dans le fil neutre est nul et donc la tension U nN = 0. Cela signifie que la résistance dans le fil neutre Z N n'affecte pas les courants de phase et ne doit pas être incluse dans les circuits pour ces séquences (Fig. 43.2 a, b). Les courants homopolaires dans toutes les phases coïncident et ne peuvent être fermés que par le fil neutre : I N = I A0 + I B0 + I C0 = 3I A0. D'après la 2e loi de Kirchhoff pour la séquence zéro (Fig. 43.1) on obtient :
U A0 = I A0 Z 0 + I N Z N = I A0 (Z 0 + 3Z N)
Selon l'équation obtenue, le circuit équivalent pour la séquence zéro recevra la forme (Fig. 43.2 c), dans laquelle la triple résistance neutre 3Z N est connectée en série avec la résistance de phase Z 0.
Dans les circuits pour composants symétriques individuels (Fig. 43.2 a, b, c), Z 1, Z 2, Z 0 sont désignés - des résistances complexes de la phase du récepteur pour les courants, respectivement, de séquences directe, inverse et zéro. Pour les récepteurs à champ magnétique tournant, ces résistances sont sensiblement différentes.

Selon la loi d'Ohm, dans chacun des circuits de la Fig. 43.2a, b, c, les courants des séquences directe, inverse et zéro sont calculés :

Les courants réels dans le circuit d'origine (Fig.43.1) sont déterminés par la méthode de superposition, sous forme de sommes vectorielles de courants de séquences directe, inverse et zéro :

Les résistances de phase complexes des récepteurs triphasés statiques (charge d'éclairage, appareils de chauffage, etc.) ne dépendent pas du type de séquence, pour de tels récepteurs Z 1 = Z 2 = Z 0. Le calcul des courants de tels récepteurs peut être effectué par des méthodes classiques. Pour les récepteurs triphasés, dans lesquels il existe un champ magnétique tournant (moteurs électriques, générateurs), les résistances de phase pour les courants de différentes séquences diffèrent considérablement (Z 1> Z 0> Z 2). Le calcul des courants de tels récepteurs avec une tension déséquilibrée doit être effectué exclusivement par la méthode des composants symétriques.
Lorsque les éléments du circuit sont connectés en série, le même courant I circule dans chacun d'eux. Par conséquent, lors de la construction de diagrammes vectoriels pour de tels circuits, le vecteur de courant est pris comme vecteur de base (initial). Les diagrammes vectoriels sont tracés au compas par la méthode serif en fonction des tensions connues d'expérience : U a - aux bornes de la résistance, U à - aux bornes de la bobine, U c - aux bornes du condensateur et U - aux bornes de l'ensemble du circuit. Toutes les valeurs des diagrammes sont dessinées à l'échelle.
A titre d'exemple, considérons la construction d'un diagramme vectoriel pour un circuit avec connexion série résistance (rhéostat) et bobine. La tension aux bornes de la résistance U a, qui est en phase avec le courant I, est tracée à l'échelle le long de la ligne de courant. A partir de la fin du vecteur de rayon égal à la tension sur la bobine U to, faites le premier cran. La deuxième encoche est réalisée avec un rayon égal à la tension totale du circuit U depuis le début du vecteur. Au point d'intersection des empattements, les extrémités des vecteurs et seront localisées (Fig. 3.14.a). Les composantes active et inductive des tensions sur la bobine sont déterminées en abaissant la perpendiculaire à l'axe du vecteur courant à partir de la fin du vecteur.
Le schéma vectoriel d'un circuit avec une connexion en série d'une bobine et d'un condensateur est construit de manière similaire et est illustré à la Fig. 3.14.b.
un B
Riz. 3.14. Construction de diagrammes vectoriels en utilisant la méthode serif.
| |
Riz. 3.15. Schéma de câblage d'un circuit électrique avec une série
en mettant sous tension la bobine et la batterie de condensateurs.
L'ordre des travaux.
1. Montez le circuit électrique selon le schéma de la fig. 3.15.
2. Réaliser une étude du phénomène de résonance des contraintes selon la méthode suivante.
En modifiant la valeur de la capacité en allumant les interrupteurs à bascule, réglez la capacité C 0, à laquelle le courant dans le circuit I et la puissance active P ont des valeurs maximales (un phénomène proche de la résonance des tensions). Mesurez la tension U dans le circuit, la tension aux bornes de la bobine U à, la tension aux bornes du condensateur U c, le courant I dans le circuit et la puissance P. Puis en changeant la capacité par pas de 1 à 2 microfarads, effectuez des mesures pour 3 - 4 points avec des capacités inférieures à C 0 , et pour 3 - 4 points pour des capacités supérieures à C 0 .
3. Les résultats de mesure pour chaque valeur de consigne de la capacité doivent être saisis dans le tableau 3.1.
Tableau 3.1
4. Selon les expériences, calculez les valeurs indiquées dans le tableau. 3.1 (impédance du circuit Z, résistance active r, réactance x, facteur de puissance du circuit cosφ, capacité x C, capacité C, impédance de la bobine z to, réactance inductive de la bobine z L, inductance de la bobine L, facteur de puissance cosφ to).
Formules de calcul
; ; ; ;
; ; ;
;
5. Selon le tableau. 3.1 construire les courbes I = f 1 (C), cosφ = f 2 (C) ; z = f 3 (C).
6. Construire des diagrammes vectoriels de courant et de tension pour trois lectures : à x L> x C, à la valeur maximale du courant dans le circuit (x L ≈x C), à x L Questions de contrôle :
1. Qu'appelle-t-on résistance inductive et capacitive et de quoi dépendent-elles ? 2. Comment l'impédance d'un circuit CA non ramifié est-elle calculée ? 3. Comment la valeur efficace du courant est-elle calculée dans un circuit avec une connexion en série d'éléments résistifs, inductifs et capacitifs ? 4. Quel est le facteur de puissance d'un circuit AC et pourquoi s'efforcer de l'augmenter lors de la consommation d'énergie électrique ? 5. Dans quelle condition une résonance de tension se produit-elle dans un circuit à courant alternatif sinusoïdal ? Comment ce phénomène est-il caractérisé ? 6. Expliquer le danger de résonance de tension dans les circuits électriques ? 7. Quel devrait être le rapport des résistances inductives et capacitives pour que le courant dans le circuit conduise la tension ? Expliquez cela avec un diagramme vectoriel. 8. Que faut-il inclure en plus dans ce circuit afin d'y obtenir une résonance de tension ? 9. Dans un circuit à courant alternatif avec une fréquence de f = 50 Hz avec une bobine connectée en série et un condensateur, une résonance se produit. Déterminez la tension aux bornes de la bobine et du condensateur si U = 20V, r = 10Ω, c = 1μF. Calculer l'inductance de la bobine. Travail 4. Connexion parallèle de l'inductance et de la capacité. Résonance des courants. but du travail: considérez les phénomènes se produisant dans un circuit à courant alternatif contenant une bobine connectée en parallèle et un condensateur (Fig. 4.1), familiarisez-vous avec la résonance des courants. Riz. 4.1. Schéma électrique avec parallèle connexion des éléments. Explications pour le travail Considérons une connexion en parallèle d'une bobine avec inductive x L = ωL et résistance active r, avec un condensateur à résistance capacitive (Fig. 4.2). Lorsqu'un tel circuit est mis sous tension sous une tension U, un courant I to apparaît dans la bobine. Riz. 4.2. Schéma d'un parallèle composés r, x L, x c où est l'impédance de la bobine. Le vecteur courant sera en retard par rapport au vecteur tension d'un angle par rapport à : ; . (4.2) Un courant I c apparaît dans le condensateur : . (4.3) Le vecteur courant c sera 90˚ en avance sur le vecteur, φ c = 90˚. Le vecteur du courant total basé sur la première loi de Kirchhoff : = İ à + İ s. (4.4) Le diagramme vectoriel des courants selon (4.4) est représenté sur la Fig. 4. Le vecteur courant to est réalisé sous un angle par rapport au vecteur tension. De la fin du vecteur courant à nous dessinons le vecteur courant c à un angle φ c = 90˚ par rapport au vecteur tension (dans le sens du plomb). La somme du vecteur à et c donnera le vecteur du courant total, en retard sur l'angle du vecteur tension. Pour la détermination analytique du courant total I et de l'angle φ, nous décomposons le courant de bobine I to en une composante active I a, qui coïncide avec la tension U, et l'inductance I L, qui est à 90˚ derrière la tension U. En divisant les côtés du triangle (Figure 4.3) par la tension U, on obtient un triangle de conductivités (Figure 4.4), à partir duquel on trouve : En changeant la valeur de la capacité C, dont dépend la valeur de b c, selon (4.7), il est possible de changer le rapport entre b c et les conductivités inductives (b L), et, par conséquent, les courants : I c = Ub c = Uωс; I L = Ub L Graphique 4.3. Diagramme vectoriel des tensions et courants pour un circuit avec parallèle connexion de la bobine et de la capacité à I L> I С Pour b C
Uωс La conductivité inductive b L prédomine et, par conséquent, le courant I L, donc le vecteur du courant total est en retard par rapport au vecteur tension (Fig. 4.3). Pour b C> b L, c'est-à-dire C> on a : Uωс La conductance capacitive b C et, par conséquent, le courant I C prévalent, donc le vecteur du courant total est en avance sur le vecteur tension (Figure 4.5). Graphique 4.4. connexion de la bobine et du condensateur à I C< I L Fig.4.5. Diagramme vectoriel pour un circuit avec parallèle connexion de la bobine et de la capacité à I C> I L À la valeur de capacité :, (4.12) la conductivité capacitive est égale à inductive : b C = c = b L, (4.13) et, par conséquent, les courants capacitif et inductif seront égaux (figure 4.6) : b C U = b L U; I C = I L. (4.14) Nous obtiendrons la résonance des courants, c'est-à-dire compensation mutuelle complète des courants inductifs et capacitifs : I C - I L = 0. (4.15) En conséquence, le courant total I à la résonance se compose uniquement du composant actif, selon l'expression (4.8) et la figure 4.6. I = I a = Ug, (4.16) par conséquent, l'angle = 0, et cos φ = 1. La conductance totale du circuit, et donc le courant I, prend une valeur minimale, puisque selon (4.10) Y = g, puisque b C - b L = 0, et la résistance totale du circuit, donc, la valeur maximale valeur. La puissance réactive du circuit est nulle : U (I C - I L) = 0; QL - QC = 0. Graphique 4.6. Diagramme vectoriel aux courants de résonance (I C = I L) Le phénomène de résonance des courants, c'est-à-dire la compensation mutuelle des courants réactifs (I C –I L = 0), et, par conséquent, les puissances réactives (Q L –Q C = 0) sont expliquées comme suit. Lorsque la branche inductive (bobine) consomme de l'énergie pour créer un champ magnétique, à ce moment dans la branche parallèle le condensateur se décharge et cède de l'énergie. Il y a une compensation mutuelle des énergies. L'énergie totale consommée du réseau est consommée uniquement sur la résistance active de la bobine (pour chauffer le fil de la bobine). La dépendance de l'impédance Z du circuit sur la valeur de la capacité sera la suivante : , (4.18) où et sont indépendants de C. Les courbes Z = f 1 (C) et I = f 2 (C), construites selon les expressions (4.18) et (4.10), sont représentées sur la figure 4.7. On donne aussi la courbe cosφ = f 3 (C), construite selon l'équation (4.11). D'après (4.12), on peut voir que les valeurs de la capacité et de l'inductance auxquelles la résonance se produit dépendent de la fréquence du courant alternatif. Avec les constantes données C et L, le phénomène de résonance peut être obtenu en changeant la fréquence. Graphique 4.7. Le graphique de la dépendance du courant dans le circuit I, cosφ et l'impédance z en fonction de la capacité. L'utilisation de diagrammes vectoriels dans le calcul et l'étude des circuits électroniques de courant alternatif permet de représenter visuellement les processus considérés et de simplifier les calculs électriques effectués. Les diagrammes vectoriels sont un ensemble de vecteurs représentant la CEM sinusoïdale effective et les courants ou leurs valeurs d'amplitude. La tension à variation harmonique est déterminée par l'expression u = U m sin ( c'est + et).
Placer en biais et par rapport à l'axe des abscisses positives x vecteur U m dont la longueur dans une échelle choisie arbitrairement est égale à l'amplitude de la quantité harmonique affichée (Fig. 1). Les angles positifs seront tracés dans le sens inverse des aiguilles d'une montre et les angles négatifs dans le sens des aiguilles d'une montre. Imaginons que le vecteur U m, à partir de l'instant t = 0, tourne autour de l'origine des coordonnées dans le sens inverse des aiguilles d'une montre avec une fréquence de rotation constante égale à la fréquence angulaire de la tension affichée. A l'instant t, le vecteur Um tourne de l'angle ωt et se placera à l'angle ωt + et par rapport à l'axe des abscisses. La projection de ce vecteur sur l'axe des ordonnées à l'échelle choisie est égale à la valeur instantanée de la tension affichée : u = U m sin ( c'est + et).
Riz. 1. Image d'une tension sinusoïdale d'un vecteur tournant Comme il s'ensuit, une quantité qui change harmonieusement dans le temps peut être représentée vecteur de rotation... Avec la phase initiale égale à zéro, lorsque u = 0, le vecteur U m pour t = 0 doit être situé sur l'axe des abscisses. Le graphique de la dépendance de toute valeur variable (y compris harmonique) au temps est appelé chronogramme... Pour les quantités harmoniques le long de l'abscisse, il est plus pratique de reporter non pas le temps t lui-même, mais la valeur proportionnelle de t. Les chronogrammes sont 100% harmoniques car ils donnent une idée de la phase, de l'amplitude et de la période d'origine. Habituellement, lors du calcul d'un circuit, nous ne nous intéressons qu'à la FEM effective, aux tensions et courants ou aux amplitudes de ces quantités, ainsi qu'à leur déphasage les uns par rapport aux autres. Par conséquent, les vecteurs fixes sont généralement considérés pour un certain moment dans le temps, qui est choisi pour que le diagramme soit agréable. Un tel diagramme s'appelle diagramme vectoriel... Avec tout ça les angles de phase sont tracés dans le sens de rotation des vecteurs (sens antihoraire), s'ils sont positifs, et dans le sens inverse, s'ils sont négatifs. Si, par exemple, l'angle de phase d'origine de la tension et est supérieur à l'angle de phase initial i, alors le déphasage φ = et- ψ i et cet angle est déposé dans le sens positif à partir du vecteur courant. Lors du calcul d'un circuit à courant alternatif, il est souvent nécessaire de définir des champs électromagnétiques, des courants ou des tensions de même fréquence. Imaginons qu'il soit nécessaire d'ajouter deux champs électromagnétiques : e 1 = E 1 m sin ( c'est + ψ
1e) et e 2 = E 2m sin ( c'est + 2e).
Cet ajout peut se faire analytiquement et graphiquement. La dernière méthode est plus intuitive et simple. Deux champs électromagnétiques ajoutés e 1 et e 2 à une certaine échelle sont représentés par les vecteurs E 1 m E 2m (Fig. 2). Lorsque ces vecteurs tournent avec la même fréquence de rotation égale à la fréquence angulaire, le placement mutuel des vecteurs tournants reste constant. Riz. 2. Ajout graphique de 2 champs électromagnétiques sinusoïdaux de fréquence similaire La somme des projections des vecteurs tournants E 1 m et E 2m sur l'axe des ordonnées est égale à la projection sur le même axe du vecteur E m, qui est leur somme géométrique. Comme il s'ensuit, lors de l'ajout de 2 champs électromagnétiques sinusoïdaux de même fréquence, il en sort un champ électromagnétique sinusoïdal de même fréquence dont l'amplitude est représentée par le vecteur E m, égal à la somme géométrique des vecteurs E 1 m et E 2m : E m = E 1 m + E 2m. Les vecteurs de champs électromagnétiques et courants alternatifs sont des images graphiques de champs électromagnétiques et de courants, par opposition aux vecteurs de grandeurs physiques qui ont une certaine signification physique : vecteurs de force, intensités de champ et autres. La méthode indiquée peut être utilisée pour ajouter et soustraire un nombre quelconque de champs électromagnétiques et de courants de même fréquence. La soustraction de 2 valeurs sinusoïdales peut être représentée comme une addition : e 1 - e 2 = e 1 + (- e 2), c'est-à-dire que la valeur réduite est additionnée à la valeur soustraite, prise avec un signe inverse. Habituellement, les diagrammes vectoriels ne sont pas construits pour les valeurs d'amplitude des champs électromagnétiques et courants alternatifs, mais pour les valeurs efficaces proportionnelles aux valeurs d'amplitude, car tous les calculs de circuit sont généralement effectués pour les champs électromagnétiques et courants efficaces. École d'électricien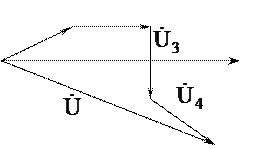 Dessinez un circuit équivalent pour lequel un diagramme vectoriel est représenté.
Dessinez un circuit équivalent pour lequel un diagramme vectoriel est représenté.
 , (4.1)
, (4.1) (4.11)
(4.11)