domicile » Fils et câbles » Fonctions trigonométriques d'un argument numérique. Propriétés et graphiques des fonctions trigonométriques Étape II

Fonctions trigonométriques d'un argument numérique. Propriétés et graphiques des fonctions trigonométriques Étape II

Nous avons examiné les fonctions trigonométriques les plus élémentaires (ne vous y trompez pas, en plus du sinus, du cosinus, de la tangente et de la cotangente, il existe de nombreuses autres fonctions, mais nous en reparlerons plus tard), mais pour l'instant nous allons considérer certaines propriétés de base des fonctions déjà étudiées.

Fonctions trigonométriques d'un argument numérique

Quel que soit le nombre réel t pris, on peut lui attribuer un nombre sin(t) défini de manière unique. Certes, la règle de correspondance est assez compliquée et consiste en ce qui suit.

Pour trouver la valeur de sin(t) par le nombre t, il vous faut :

positionnez le cercle numérique sur le plan de coordonnées de sorte que le centre du cercle coïncide avec l'origine et que le point de départ A du cercle atteigne le point (1; 0);
trouver un point sur le cercle correspondant au nombre t ;
trouver l'ordonnée de ce point.
cette ordonnée est le sin(t) recherché.

En fait, nous parlons de la fonction s = sin(t) , où t est un nombre réel quelconque. Nous pouvons calculer certaines valeurs de cette fonction (par exemple, sin(0) = 0 , \(sin \frac (\pi)(6) = \frac(1)(2) \) etc.), nous connaissons certaines de ses propriétés.

De la même manière, nous pouvons supposer que nous avons déjà reçu quelques idées sur trois autres fonctions : s = cos(t) s = tg(t) s = ctg(t) Toutes ces fonctions sont appelées fonctions trigonométriques d'argument numérique t .

Connexion des fonctions trigonométriques

Comme vous, j'espère, devinez que toutes les fonctions trigonométriques sont interconnectées et même sans connaître la valeur de l'une, on peut la trouver à travers l'autre.

Par exemple, la formule la plus importante de toute la trigonométrie est identité trigonométrique de base:

\[ sin^(2) t + cos^(2) t = 1 \]

Comme vous pouvez le voir, connaissant la valeur du sinus, vous pouvez trouver la valeur du cosinus, et vice versa. Formules également très courantes reliant le sinus et le cosinus à la tangente et à la cotangente :

\[ \boxed (\tan\; t=\frac(\sin\; t)(\cos\; t), \qquad t \neq \frac(\pi)(2)+ \pi k) \]

\[ \boxed (\cot\; t=\frac(\cos\; )(\sin\; ), \qquad t \neq \pi k) \]

Des deux dernières formules, une autre identité trigométrique peut être déduite, reliant cette fois la tangente et la cotangente :

\[ \boxed (\tan \; t \cdot \cot \; t = 1, \qquad t \neq \frac(\pi k)(2)) \]

Voyons maintenant comment ces formules fonctionnent en pratique.

EXEMPLE 1. Simplifiez l'expression : a) \(1+ \tan^2 \; t \), b) \(1+ \cot^2 \; t \)

a) Tout d'abord, on écrit la tangente en gardant le carré :

\[ 1+ \tan^2 \; t = 1 + \frac(\sin^2 \; t)(\cos^2 \; t) \]

\[ 1 + \frac(\sin^2 \; t)(\cos^2 \; t)= \sin^2\; t + \cos^2 \ ; t + \frac(\sin^2 \; t)(\cos^2 \; t) \]

Maintenant on introduit tout sous un dénominateur commun, et on obtient :

\[ \sin^2\ ; t + \cos^2 \ ; t + \frac(\sin^2 \; t)(\cos^2 \; t) = \frac(\cos^2 \; t + \sin^2 \; t)(\cos^2 \; t )\]

Et enfin, comme on le voit, le numérateur peut être réduit à un selon l'identité trigonométrique de base, en conséquence on obtient : \[ 1+ \tan^2 \; = \frac(1)(\cos^2 \; t) \]

b) Avec la cotangente, nous effectuons toutes les mêmes actions, seul le dénominateur n'aura plus de cosinus, mais un sinus, et la réponse se présentera ainsi :

\[ 1+ \lit bébé^2 \; = \frac(1)(\sin^2 \; t) \]

Après avoir terminé cette tâche, nous avons dérivé deux autres formules très importantes qui relient nos fonctions, que vous devez également connaître sur le bout des doigts :

\[ \boxed (1+ \tan^2 \; = \frac(1)(\cos^2 \; t), \qquad t \neq \frac(\pi)(2)+ \pi k) \]

\[ \boxed (1+ \cot^2 \; = \frac(1)(\sin^2 \; t), \qquad t \neq \pi k) \]

Vous devez connaître par cœur toutes les formules présentées dans le cadre, sinon une étude plus approfondie de la trigonométrie sans elles est tout simplement impossible. À l'avenir, il y aura plus de formules et il y en aura beaucoup, et je vous assure que vous vous en souviendrez certainement pendant longtemps, ou peut-être que vous ne vous en souviendrez pas, mais TOUT LE MONDE devrait connaître ces six pièces !

Javascript est désactivé sur votre navigateur.
Les contrôles ActiveX doivent être activés pour effectuer des calculs !

La leçon vidéo "Fonctions trigonométriques d'un argument numérique" est un matériel visuel pour assurer la clarté lors de l'explication du sujet de la leçon. Au cours de la démonstration, le principe de formation de la valeur des fonctions trigonométriques à partir d'un nombre est considéré, un certain nombre d'exemples sont décrits qui enseignent comment calculer les valeurs des fonctions trigonométriques à partir d'un nombre. Avec l'aide de ce manuel, il est plus facile de former des compétences dans la résolution de problèmes pertinents, pour parvenir à la mémorisation du matériel. L'utilisation du manuel augmente l'efficacité de la leçon, contribue à la réalisation rapide des objectifs d'apprentissage.

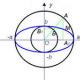
Le titre du sujet est indiqué au début de la leçon. Ensuite, la tâche consiste à trouver le cosinus correspondant à un argument numérique. On note que ce problème est résolu simplement et cela peut être clairement démontré. L'écran affiche un cercle unité centré à l'origine. En même temps, on a remarqué que le point d'intersection du cercle avec le demi-axe positif de l'axe des abscisses est situé au point A (1 ; 0). Un exemple de point M est donné, qui représente l'argument t=π/3. Ce point est marqué sur le cercle unité, et une perpendiculaire à l'axe des abscisses en descend. L'abscisse trouvée du point est le cosinus cos t. Dans ce cas, l'abscisse du point sera x=1/2. Donc cos t=1/2.

En résumant les faits considérés, on note qu'il est logique de parler de la fonction s=cos t. Il est à noter que les étudiants ont déjà des connaissances sur cette fonction. Certaines valeurs de cosinus cos 0=1, cos π/2=0, cos π/3=1/2 sont calculées. Sont également liées à cette fonction les fonctions s=sin t, s=tg t, s=ctg t. Il est à noter qu'ils ont un nom commun pour tous - les fonctions trigonométriques.

Des relations importantes sont démontrées qui sont utilisées dans la résolution de problèmes avec des fonctions trigonométriques : l'identité de base sin 2 t+ cos 2 t=1, l'expression de la tangente et de la cotangente en termes de sinus et de cosinus tg t=sin t/cos t, où t≠ π/2+πk pour kϵZ, ctg t= cos t/sin t, où t≠πk pour kϵZ, ainsi que le rapport tangente sur cotangente tg t ctg t=1 où t≠πk/2 pour kϵZ.

De plus, il est proposé de considérer la preuve de la relation 1+ tan 2 t=1/ cos 2 t, avec t≠π/2+πk pour kϵZ. Pour prouver l'identité, il faut représenter tg 2 t comme un rapport de sinus et cosinus, puis ramener les termes du côté gauche à un dénominateur commun 1+ tg 2 t=1+sin 2 t/cos 2 t = (sin 2 t+cos 2 t )/ cos 2 t. En utilisant l'identité trigonométrique de base, nous obtenons 1 au numérateur, c'est-à-dire l'expression finale 1/ cos 2 t. Q.E.D.

L'identité 1+ ctg 2 t=1/ sin 2 t se démontre de façon similaire, avec t≠πk pour kϵZ. Tout comme dans la preuve précédente, la cotangente est remplacée par le rapport correspondant du cosinus et du sinus, et les deux termes du côté gauche sont réduits à un dénominateur commun 1+ ctg 2 t=1+ cos 2 t/sin 2 t= ( sin 2 t+cos 2 t)/sin2t. Après avoir appliqué l'identité trigonométrique de base au numérateur, nous obtenons 1/ sin 2 t. C'est l'expression recherchée.

La solution d'exemples est considérée, dans laquelle les connaissances acquises sont appliquées. Dans la première tâche, vous devez trouver les valeurs de cost, tgt, ctgt, si le sinus du nombre sint=4/5 est connu, et t appartient à l'intervalle π/2< t<π. Для нахождения косинуса в данном примере рекомендуется использовать тождество sin 2 t+ cos 2 t=1, из которого следует cos 2 t=1-sin 2 t. Зная значение синуса, можно найти косинус cos 2 t=1-(4/5) 2 =9/25. То есть значение косинуса cost=3/5 и cost=-3/5. В условии указано, что аргумент принадлежит второй четверти координатной плоскости. В этой четверти значение косинуса отрицательное. С учетом данного ограничения находим cost=-3/5. Для нахождения тангенса числа пользуемся его определением tgt= sint/cost. Подставив известные значения синуса и косинуса, получаем tgt=4/5:(-3/5)=-4/3. Чтобы найти значение котангенса, также используется определение котангенса ctgt= cost/sint. Подставив известные значения синуса и косинуса в отношение, получаем ctgt=(-3/5):4/5=-3/4.

Ensuite, nous considérons la solution d'un problème similaire dans lequel la tangente cible=-8/15 est connue, et l'argument est limité aux valeurs 3π/2

Pour trouver la valeur du sinus, on utilise la définition de la tangente cible = sint / coût. De là, nous trouvons sint= tgt cost=(-8/15)(15/17)=-8/17. Sachant que la cotangente est la fonction inverse de la tangente, on trouve ctgt=1/(-8/15)=-15/8.

La leçon vidéo "Fonctions trigonométriques d'un argument numérique" est utilisée pour augmenter l'efficacité d'une leçon de mathématiques à l'école. Au cours de l'apprentissage à distance, ce matériel peut être utilisé comme aide visuelle pour la formation de compétences en résolution de problèmes, où il existe des fonctions trigonométriques d'un nombre. Pour acquérir ces compétences, il peut être recommandé à l'étudiant d'examiner de manière indépendante le matériel visuel.

INTERPRÉTATION DU TEXTE :

Le sujet de la leçon est "Fonctions trigonométriques d'un argument numérique".

Tout nombre réel t peut être associé à un nombre défini de manière unique cos t. Pour ce faire, vous devez effectuer les étapes suivantes :

1) sur le plan des coordonnées, positionnez le cercle numérique de sorte que le centre du cercle coïncide avec l'origine des coordonnées et que le point de départ A du cercle atteigne le point (1; 0);

2) trouver un point sur le cercle qui correspond au nombre t ;

3) trouver l'abscisse de ce point. C'est un coût.

Par conséquent, nous parlerons de la fonction s \u003d coût t (es est égal au cosinus de te), où t est n'importe quel nombre réel. Nous avons déjà une idée de cette fonction :

appris à calculer certaines valeurs, par exemple, cos 0=1, cos = 0, cos =, etc. (le cosinus de zéro est égal à un, le cosinus de pi par deux est égal à zéro, le cosinus de pi par trois est égal à une seconde, et ainsi de suite).
et puisque les valeurs de sinus, cosinus, tangente et cotangente sont interconnectées, nous avons eu une idée de trois autres fonctions : s= sint ; s=cible ; s=ctgt. (es est égal au sinus de te, es est égal à la tangente de te, es est égal à la cotangente de te)

Toutes ces fonctions sont appelées fonctions trigonométriques d'argument numérique t.

À partir des définitions de sinus, cosinus, tangente et cotangente, certaines relations suivent :

1) sin 2 t + cos 2 t = 1 (sinus au carré te plus cosinus au carré te égale un)

2) cible = à t ≠ + πk, kϵZ

3) ctgt = à t ≠ πk, kϵZ (la cotangente de te est égale au rapport du cosinus de te au sinus de te lorsque te n'est pas égal au pic de ka, qui appartient à z).

4)cible ∙ ctgt = 1 pour t ≠ , kϵZ

Nous démontrons deux formules plus importantes :

Un plus le carré tangent de te est égal au rapport de un au cosinus carré de te lorsque te n'est pas égal à pi par deux plus pi.

Preuve.

L'unité d'expression plus le carré tangent te, nous la réduirons à un dénominateur commun cosinus carré te. On obtient au numérateur la somme des carrés du cosinus de te et du sinus de te, qui est égal à un. Et le dénominateur reste le carré du cosinus te.

La somme de l'unité et du carré de la cotangente te est égale au rapport de l'unité au carré du sinus de te lorsque te n'est pas égal au pic.

Preuve.

L'unité d'expression plus la cotangente au carré te, de même, nous la réduisons à un dénominateur commun et appliquons la première relation.

Prenons des exemples.

EXEMPLE 1. Trouver cost, tgt, ctgt si sint = et< t < π.(если синус тэ равен четырем пятым и тэ из промежутка от пи на два до пи)

Solution. À partir de la première relation, nous trouvons le cosinus carré te égal à un moins le sinus carré te: cos 2 t \u003d 1 - sin 2 t.

Ainsi, cos 2 t = 1 -() 2 = (le cosinus du carré de te est neuf vingt-cinquièmes), c'est-à-dire coût = (le cosinus de te est égal à trois cinquièmes) ou coût = - (le cosinus de te est égal à moins trois cinquièmes). Par condition, l'argument t appartient au deuxième quart, et en lui coûte t< 0 (косинус тэ отрицательный).

Ainsi, le cosinus te est égal à moins les trois cinquièmes, coût = - .

Calculer la tangente te :

tgt = = ׃ (-)= - ;(la tangente de te est égale au rapport du sinus de te au cosinus de te, ce qui signifie quatre cinquièmes à moins trois cinquièmes et est égal à moins quatre tiers)

En conséquence, on calcule (la cotangente du nombre te, puisque la cotangente de te est égale au rapport du cosinus de te au sinus de te,) ctgt = = - .

(la cotangente de te est moins les trois quarts).

Réponse : coût = - , cible= - ; ctgt = - . (La réponse sera remplie à votre guise)

EXEMPLE 2. On sait que cible = - et< t < 2π(тангенс тэ равен минус восемь пятнадцатых и тэ принадлежит промежутку от трех пи на два до двух пи). Найти значения cost, sint, ctgt.

Solution. Nous utilisons ce rapport, en remplaçant la valeur dans cette formule, nous obtenons :

1 + (-) 2 \u003d (un par cosinus carré de te est égal à la somme de un et du carré moins huit quinzièmes). De là, nous trouvons cos 2 t =

(le cosinus carré de te est deux cent vingt-cinq deux cent quatre-vingt-neuvièmes). Donc coût = (cosinus te est égal à quinze dix-septièmes) ou

coût = . Par condition, l'argument t appartient au quatrième trimestre, où coût > 0. Par conséquent, coût = .(cosenus te est quinze dix-septièmes)

Trouver la valeur de l'argument sinus te. Puisque d'après le rapport (montrer le rapport cible = à t ≠ + πk, kϵZ) le sinus de te est égal au produit de la tangente de te par le cosinus de te, puis en substituant la valeur de l'argument te..la tangente de te est égal à moins huit quinzièmes .. par condition, et le cosinus de te est égal à résolu plus tôt, on obtient

sint = cible ∙ coût = (-) ∙ = - , (le sinus de te est égal à moins huit dix-septièmes)

ctgt == - . (puisque la cotangente de te est l'inverse de la tangente, cela signifie que la cotangente de te est moins quinze dix-huitième)

Quel que soit le nombre réel t pris, on peut lui attribuer un nombre sin t défini de manière unique. Certes, la règle de correspondance est assez compliquée ; comme nous l'avons vu plus haut, elle consiste en ce qui suit.

Pour trouver la valeur de sin t par le nombre t, il vous faut :

1) positionner le cercle numérique dans le plan de coordonnées de sorte que le centre du cercle coïncide avec l'origine et que le point de départ A du cercle rencontre le point (1 ; 0) ;

2) trouver un point sur le cercle correspondant au nombre t ;

3) trouver l'ordonnée de ce point.

Cette ordonnée est sin t.

En fait, nous parlons de la fonction u = sin t, où t est un nombre réel quelconque.

Toutes ces fonctions sont appelées fonctions trigonométriques de l'argument numérique t.

Il existe un certain nombre de relations reliant les valeurs de diverses fonctions trigonométriques, nous avons déjà reçu certaines de ces relations :

sin 2 t + cos 2 t = 1

A partir des deux dernières formules, il est facile d'obtenir une relation reliant tg t et ctg t :

Toutes ces formules sont utilisées dans les cas où, connaissant la valeur d'une fonction trigonométrique, il est nécessaire de calculer les valeurs des fonctions trigonométriques restantes.

Les termes « sinus », « cosinus », « tangente » et « cotangente » étaient en fait familiers, cependant, ils étaient encore utilisés dans une interprétation légèrement différente : en géométrie et en physique, ils considéraient le sinus, le cosinus, la tangente et la cotangente. g la une(mais non

chiffres, comme dans les paragraphes précédents).

Il est connu de la géométrie que le sinus (cosinus) d'un angle aigu est le rapport de la jambe d'un triangle rectangle à son hypoténuse, et la tangente (cotangente) d'un angle est le rapport des jambes d'un triangle rectangle. Une approche différente des concepts de sinus, cosinus, tangente et cotangente a été développée dans les paragraphes précédents. En fait, ces approches sont interdépendantes.

Prenons un angle avec une mesure de degré b o et organisons-le dans le modèle "cercle numérique dans un système de coordonnées rectangulaires" comme indiqué sur la Fig. 14

dessus d'angle compatible avec le centre

cercles (avec l'origine du système de coordonnées),

et un côté du coin est compatible avec

rayon positif de l'axe des abscisses. point

intersection de l'autre côté de l'angle avec

le cercle sera désigné par la lettre M. Ordina-

Figure 14 b o , et l'abscisse de ce point est le cosinus de l'angle b o .

Pour trouver le sinus ou le cosinus de l'angle b o il n'est nullement nécessaire de faire à chaque fois ces constructions très complexes.

Il suffit de noter que l'arc AM est la même partie de la longueur du cercle numérique que l'angle b o est de l'angle de 360°. Si la longueur de l'arc AM est notée par la lettre t, alors on obtient :

De cette façon,

Par exemple,

On pense que 30° est une mesure en degré d'un angle, et est une mesure en radian du même angle : 30° = rad. En général:

En particulier, je suis heureux d'où, à son tour, nous obtenons.

Alors, qu'est-ce que 1 radian ? Il existe différentes mesures de longueur de segment : centimètres, mètres, yards, etc. Il existe également diverses mesures pour indiquer la grandeur des angles. On considère les angles au centre du cercle unité. Un angle de 1° est un angle au centre basé sur un arc faisant partie d'un cercle. Un angle de 1 radian est un angle au centre basé sur un arc de longueur 1, c'est-à-dire sur un arc dont la longueur est égale au rayon du cercle. De la formule, nous obtenons que 1 rad \u003d 57,3 °.

En considérant la fonction u = sin t (ou toute autre fonction trigonométrique), on peut considérer la variable indépendante t comme un argument numérique, comme c'était le cas dans les paragraphes précédents, mais on peut aussi considérer cette variable comme une mesure de l'angle, c'est à dire argumentation angulaire. Par conséquent, parlant d'une fonction trigonométrique, il est en un certain sens indifférent de la considérer comme une fonction d'un argument numérique ou angulaire.

Dans ce chapitre, nous allons introduire les fonctions trigonométriques d'un argument numérique. De nombreuses questions en mathématiques, mécanique, physique et autres sciences conduisent à des fonctions trigonométriques non seulement de l'angle (arc), mais aussi d'arguments de toute autre nature (longueur, temps, température, etc.). Jusqu'à présent, l'argument d'une fonction trigonométrique a été compris comme un angle mesuré en degrés ou en radians. Nous généralisons maintenant les concepts de sinus, cosinus, tangente, cotangente, sécante et cosécante en les introduisant comme fonctions d'un argument numérique.

Définition. Les fonctions trigonométriques d'un argument numérique sont les fonctions trigonométriques du même nom d'un angle égal à des radians.

Précisons cette définition par des exemples concrets.

Exemple 1. Calculez la valeur de . Ici, nous entendons un nombre irrationnel abstrait. Par définition. Alors, .

Exemple 2. Calculez la valeur de . Ici, par 1,5, nous entendons un nombre abstrait. Tel que défini (voir annexe II).

Exemple 3. Calculer la valeur Comme pour le précédent, on obtient (voir annexe II).

Ainsi, à l'avenir, sous l'argument des fonctions trigonométriques, nous comprendrons l'angle (arc) ou juste un nombre, selon le problème que nous résolvons. Et dans certains cas, l'argument peut être une valeur qui a une autre dimension, comme le temps, etc. En appelant l'argument un angle (arc), nous pouvons entendre par lui le nombre avec lequel il est mesuré en radians.

Objectifs de la leçon:

Éducatif:

Fournir la répétition, la généralisation et la systématisation du matériel du sujet « Fonctions trigonométriques d'un argument numérique » ;
Créer les conditions de contrôle (contrôle de soi) de l'assimilation des savoirs et des compétences.

Développement:

Contribuer à la formation de la capacité d'appliquer des techniques - comparaisons, généralisations, mise en évidence de l'essentiel, transfert de connaissances à une nouvelle situation;
Développement des perspectives mathématiques, de la pensée, de la parole, de l'attention et de la mémoire.

Éducatif:

Promouvoir l'éducation d'intérêt pour les mathématiques, l'activité, les compétences en communication et une culture commune.

Type de leçon : leçon de généralisation et de systématisation des connaissances.

Méthodes d'enseignement: recherche partielle, (heuristique).

Test de vérification du niveau de connaissances, résolution de problèmes cognitifs généralisants, auto-examen, généralisations du système.

Plan de cours.

Org. moment - 2 min.
Test d'autocontrôle - 10 min.
Reportage sur le sujet - 3 min.
Systématisation du matériel théorique - 15 min.
Travail indépendant différencié avec auto-examen - 10 min.
Le résultat d'un travail indépendant - 2 min.
Résumé de la leçon - 3 min.

Pendant les cours

1. Moment organisationnel.

Devoirs:

Paragraphe 1, paragraphe 1.4
- Travail de test (des tâches ont été affichées sur le stand).

L'écrivain français Anatole France a dit un jour : « Apprendre ne peut être qu'amusant. Pour digérer la connaissance, il faut l'absorber avec enthousiasme. Suivons ce conseil de l'écrivain aujourd'hui dans la leçon, soyons actifs, attentifs, absorbons les connaissances avec un grand désir. Après tout, ils vous seront utiles à l'avenir.

Aujourd'hui, nous avons la dernière leçon sur le sujet : "Fonctions trigonométriques d'un argument numérique". Nous répétons, généralisons le matériel étudié, les méthodes et les techniques de résolution des expressions trigonométriques.

2. Test d'autocontrôle.

Le travail est réalisé en deux versions. questions à l'écran.

№	1 option	Option 2
1	Définir le sinus et le cosinus d'un angle aigu	Définir la tangente et la cotangente d'un angle aigu
2	Quelles fonctions numériques sont appelées tangente et cotangente ? Donnez une définition.	Quelles fonctions numériques sont appelées sinus et cosinus ? Donnez une définition.
3	Un point sur le cercle unité a pour coordonnées . Trouver les valeurs de sin, cos.	Le point du cercle unitaire a pour coordonnées (-0,8 ; -0,6). Trouvez la valeur tg , ctg .
4	Parmi les fonctions trigonométriques de base, lesquelles sont impaires ? Écris les égalités correspondantes.	Parmi les fonctions trigonométriques de base, lesquelles sont paires ? Écris les égalités correspondantes.
5	Comment les valeurs du sinus et du cosinus changent-elles lorsque l'angle change d'un nombre entier de tours ? Écris les égalités correspondantes.	Comment les valeurs de la tangente et de la cotangente changent-elles lorsque l'angle change d'un nombre entier de tours ? Quelle est la fonctionnalité ? Écris les égalités correspondantes.
6	Trouver les valeurs sin cos, sin(- 630°), cos (- 630°).	Trouver les valeurs tg , ctg , tg 540°, ctg(-450°).
7	Quelle figure montre le graphique de la fonction y \u003d sin x ?	Quelle figure montre le graphique de la fonction y \u003d tg x ?
8	Notez les formules de réduction des angles ( - ), (- ).	Notez les formules de réduction des angles (+ ), (+ ).
9	Ecrire des formules d'addition.	Écrire des identités trigonométriques de base.
10	Écrivez des formules pour abaisser le degré.	Ecrire des formules à double argument.

Les élèves marquent les mauvaises étapes. Le nombre de bonnes réponses est enregistré dans la fiche de connaissances.

3. Message.

Rapport sur l'histoire du développement de la trigonométrie (un étudiant formé parle).

4. Systématisation du matériel théorique.

devoirs oraux.

1) De quoi parle-t-on ? Quelle est la particularité ?

Déterminez le signe de l'expression :

a) cos (700°) tg 380°,
b) cos (- 1) sin (- 2)

2) Que dit ce bloc de formules ? Où est l'erreur ?

3) Considérez le tableau :

Transformations trigonométriques
Trouver les valeurs d'expressions trigonométriques	Trouver la valeur d'une fonction trigonométrique à partir d'une valeur connue d'une fonction trigonométrique donnée	Simplifier les expressions trigonométriques	Identités

4) Résoudre des problèmes de chaque type de transformations trigonométriques.

Trouver les valeurs des expressions trigonométriques.