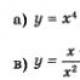Fonctions paires et impaires. Parité des fonctions

Masquer Afficher

Façons de définir une fonction

Soit la fonction donnée par la formule : y=2x^(2)-3 . En attribuant n'importe quelle valeur à la variable indépendante x , vous pouvez utiliser cette formule pour calculer les valeurs correspondantes de la variable dépendante y . Par exemple, si x=-0.5 , alors en utilisant la formule, nous obtenons que la valeur correspondante de y est y=2 \cdot (-0.5)^(2)-3=-2.5 .

Étant donné toute valeur prise par l'argument x dans la formule y=2x^(2)-3 , une seule valeur de fonction peut être calculée qui lui correspond. La fonction peut être représentée sous forme de tableau :

X	−2	−1	0	1	2	3
y	−4	−3	−2	−1	0	1

En utilisant ce tableau, vous pouvez comprendre que pour la valeur de l'argument -1, la valeur de la fonction -3 correspondra ; et la valeur x=2 correspondra à y=0, et ainsi de suite. Il est également important de savoir que chaque valeur d'argument dans le tableau correspond à une seule valeur de fonction.

D'autres fonctions peuvent être définies à l'aide de graphiques. À l'aide du graphique, il est établi quelle valeur de la fonction est en corrélation avec une certaine valeur de x. Le plus souvent, il s'agira d'une valeur approximative de la fonction.

Fonction pair et impair

La fonction est même fonction, lorsque f(-x)=f(x) pour tout x du domaine. Une telle fonction sera symétrique par rapport à l'axe Oy.

La fonction est fonction impaire lorsque f(-x)=-f(x) pour tout x du domaine. Une telle fonction sera symétrique par rapport à l'origine O (0;0) .

La fonction est pas même, ni impair et appelé fonction générale lorsqu'il n'a pas de symétrie autour de l'axe ou de l'origine.

Nous examinons la fonction suivante pour la parité :

f(x)=3x^(3)-7x^(7)

D(f)=(-\infty ; +\infty) avec un domaine de définition symétrique autour de l'origine. f(-x)= 3 \cdot (-x)^(3)-7 \cdot (-x)^(7)= -3x^(3)+7x^(7)= -(3x^(3)-7x^(7))= -f(x).

Par conséquent, la fonction f(x)=3x^(3)-7x^(7) est impaire.

Fonction périodique

La fonction y=f(x) , dans le domaine de laquelle f(x+T)=f(x-T)=f(x) est vraie pour tout x, s'appelle fonction périodique de période T \neq 0 .

Répétition du graphique de la fonction sur tout segment de l'axe des abscisses, qui a une longueur T .

Intervalles où la fonction est positive, c'est-à-dire f (x) > 0 - segments de l'axe des abscisses, qui correspondent aux points du graphique de la fonction situés au-dessus de l'axe des abscisses.

f(x) > 0 sur (x_(1); x_(2)) \cup (x_(3); +\infty)

Écarts où la fonction est négative, c'est-à-dire f(x)< 0 - отрезки оси абсцисс, которые отвечают точкам графика функции, лежащих ниже оси абсцисс.

f(x)< 0 на (-\infty; x_(1)) \cup (x_(2); x_(3))

Limitation de fonction

délimité par le bas il est d'usage d'appeler une fonction y=f(x), x \in X lorsqu'il existe un nombre A pour lequel l'inégalité f(x) \geq A est vraie pour tout x \in X .

Un exemple de fonction délimitée ci-dessous : y=\sqrt(1+x^(2)) puisque y=\sqrt(1+x^(2)) \geq 1 pour tout x .

borné d'en haut une fonction y=f(x), x \in X est appelée s'il existe un nombre B pour lequel l'inégalité f(x) \neq B est vraie pour tout x \in X .

Un exemple de fonction délimitée ci-dessous : y=\sqrt(1-x^(2)), x \in [-1;1] puisque y=\sqrt(1+x^(2)) \neq 1 pour tout x \in [-1;1] .

Limité il est d'usage d'appeler une fonction y=f(x), x \in X lorsqu'il existe un nombre K > 0 pour lequel l'inégalité \left | f(x) \right | \neq K pour tout x \in X .

Exemple de fonction bornée : y=\sin x est borné sur la droite entière car \gauche | \sin x \right | \neq 1.

Fonction croissante et décroissante

Il est d'usage de parler d'une fonction qui augmente sur l'intervalle considéré comme fonction croissante lorsqu'une plus grande valeur de x correspondra à une plus grande valeur de la fonction y=f(x) . De là, il s'avère qu'en prenant dans l'intervalle considéré deux valeurs arbitraires de l'argument x_(1) et x_(2) , et x_(1) > x_(2) , ce sera y(x_(1)) > y(x_(2)) .

Une fonction décroissante sur l'intervalle considéré est appelée fonction décroissante lorsqu'une plus grande valeur de x correspondra à une plus petite valeur de la fonction y(x) . De là, il s'avère qu'en prenant dans l'intervalle considéré deux valeurs arbitraires de l'argument x_(1) et x_(2) , et x_(1) > x_(2) , ce sera y(x_(1))< y(x_{2}) .

Racines de fonction il est d'usage de nommer les points d'intersection de la fonction F=y(x) avec l'axe des abscisses (ils sont obtenus à la suite de la résolution de l'équation y(x)=0 ).

a) Si une fonction paire augmente pour x > 0, alors elle diminue pour x< 0

b) Lorsqu'une fonction paire diminue pour x > 0, alors elle augmente pour x< 0

c) Lorsqu'une fonction impaire augmente pour x > 0, alors elle augmente aussi pour x< 0

d) Lorsqu'une fonction impaire décroît pour x > 0, alors elle décroît aussi pour x< 0

Fonctions extrêmes

Point minimum de la fonction y=f(x) il est d'usage d'appeler un tel point x=x_(0) , dans lequel son voisinage aura d'autres points (sauf le point x=x_(0) ), et pour eux alors l'inégalité f( x) > f (x_(0)) . y_(min) - désignation de la fonction au point min.

Point maximum de la fonction y=f(x) il est d'usage d'appeler un tel point x=x_(0) , dans lequel son voisinage aura d'autres points (sauf le point x=x_(0) ), puis l'inégalité f(x) sera satisfait pour eux< f(x^{0}) . y_{max} - обозначение функции в точке max.

Condition nécessaire

D'après le théorème de Fermat : f"(x)=0, alors lorsque la fonction f(x) , qui est dérivable au point x_(0) , un extremum apparaîtra en ce point.

Condition suffisante

1. Lorsque le signe de la dérivée passe de plus à moins, alors x_(0) sera le point minimum ;
2. x_(0) - sera un point maximum uniquement lorsque la dérivée change de signe de moins à plus en passant par le point stationnaire x_(0) .

La plus grande et la plus petite valeur de la fonction sur l'intervalle

Étapes de calcul :

1. Recherche de la dérivée f"(x) ;
2. Les points stationnaires et critiques de la fonction sont trouvés et ceux appartenant à l'intervalle sont choisis;
3. Les valeurs de la fonction f(x) se trouvent aux points et extrémités stationnaires et critiques du segment. Le plus petit des résultats sera la plus petite valeur de la fonction, et plus - le plus grand.

Qui à un degré ou à un autre vous étaient familiers. Il y a également été noté que le stock de biens de fonction sera progressivement reconstitué. Deux nouvelles propriétés seront abordées dans cette section.

Définition 1.

La fonction y \u003d f (x), x є X, est appelée même si pour toute valeur x de l'ensemble X l'égalité f (-x) \u003d f (x) est vraie.

Définition 2.

La fonction y \u003d f (x), x є X, est dite impaire si pour toute valeur x de l'ensemble X l'égalité f (-x) \u003d -f (x) est vraie.

Montrer que y = x 4 est une fonction paire.

Solution. Nous avons: f (x) \u003d x 4, f (-x) \u003d (-x) 4. Mais (-x) 4 = x 4 . Donc, pour tout x, l'égalité f (-x) = f (x), c'est-à-dire la fonction est paire.

De même, on peut prouver que les fonctions y - x 2, y \u003d x 6, y - x 8 sont paires.

Montrer que y = x 3 est une fonction impaire.

Solution. Nous avons: f (x) \u003d x 3, f (-x) \u003d (-x) 3. Mais (-x) 3 = -x 3 . D'où, pour tout x, l'égalité f (-x) \u003d -f (x), c'est-à-dire la fonction est impaire.

De même, on peut prouver que les fonctions y \u003d x, y \u003d x 5, y \u003d x 7 sont impaires.

Vous et moi nous sommes convaincus à plusieurs reprises que les nouveaux termes en mathématiques ont le plus souvent une origine "terrestre", c'est-à-dire ils peuvent être expliqués d'une manière ou d'une autre. C'est le cas pour les fonctions paires et impaires. Voir: y - x 3, y \u003d x 5, y \u003d x 7 sont des fonctions impaires, tandis que y \u003d x 2, y \u003d x 4, y \u003d x 6 sont des fonctions paires. Et en général, pour toute fonction de la forme y \u003d x "(ci-dessous, nous étudierons spécifiquement ces fonctions), où n est un nombre naturel, nous pouvons conclure: si n est un nombre impair, alors la fonction y \u003d x " est impair; si n est un nombre pair, alors la fonction y = xn est paire.

Il existe également des fonctions qui ne sont ni paires ni impaires. Telle, par exemple, est la fonction y \u003d 2x + 3. En effet, f (1) \u003d 5, et f (-1) \u003d 1. Comme vous pouvez le voir, ici Par conséquent, ni l'identité f (-x ) \u003d f ( x), ni l'identité f(-x) = -f(x).

Ainsi, une fonction peut être paire, impaire ou ni l'une ni l'autre.

L'étude de la question de savoir si une fonction donnée est paire ou impaire est généralement appelée l'étude de la fonction de parité.

Les définitions 1 et 2 traitent des valeurs de la fonction aux points x et -x. Cela suppose que la fonction est définie à la fois au point x et au point -x. Cela signifie que le point -x appartient au domaine de la fonction en même temps que le point x. Si un ensemble numérique X avec chacun de ses éléments x contient l'élément opposé -x, alors X est appelé un ensemble symétrique. Disons que (-2, 2), [-5, 5], (-oo, +oo) sont des ensembles symétriques, tandis que ; (∞;∞) sont des ensembles symétriques, et , [–5;4] sont non symétriques.

- Les fonctions paires ont-elles un domaine de définition - un ensemble symétrique ? Les impairs ?
- Si D( F) est un ensemble asymétrique, alors quelle est la fonction ?
– Ainsi, si la fonction à = F(X) est pair ou impair, alors son domaine de définition est D( F) est un ensemble symétrique. Mais l'inverse est-il vrai, si le domaine d'une fonction est un ensemble symétrique, alors il est pair ou impair ?
- Donc la présence d'un ensemble symétrique du domaine de définition est une condition nécessaire, mais pas suffisante.
– Alors, comment pouvons-nous étudier la fonction de parité ? Essayons d'écrire un algorithme.

Glisser

Algorithme d'examen d'une fonction pour la parité

1. Déterminez si le domaine de la fonction est symétrique. Sinon, la fonction n'est ni paire ni impaire. Si oui, passez à l'étape 2 de l'algorithme.

2. Écrivez une expression pour F(–X).

3. Comparez F(–X).et F(X):

• si F(–X).= F(X), alors la fonction est paire ;
• si F(–X).= – F(X), alors la fonction est impaire ;
• si F(–X) ≠ F(X) et F(–X) ≠ –F(X), alors la fonction n'est ni paire ni impaire.

Exemples:

Étudier la fonction de parité a) à=x5+ ; b) à= ; v) à= .

Solution.

a) h (x) \u003d x 5 +,

1) D(h) = (–∞; 0) U (0; +∞), ensemble symétrique.

2) h (- x) \u003d (-x) 5 + - x5 - \u003d - (x 5 +),

3) h (- x) \u003d - h (x) \u003d\u003e fonction h(x)= x 5 + impair.

b) y =,

à = F(X), D(f) = (–∞; –9) ? (–9 ; +∞), ensemble asymétrique, donc la fonction n'est ni paire ni impaire.

v) F(X) = , y = f(x),

1) D( F) = (–∞; 3] ≠ ; b) (∞; –2), (–4; 4] ?

Option 2

1. L'ensemble donné est-il symétrique : a) [–2;2] ; b) (∞ ; 0], (0 ; 7) ?

une); b) y \u003d x (5 - x 2). 2. Examinez la fonction de parité :

a) y \u003d x 2 (2x - x 3), b) y \u003d

3. Dans la fig. comploté à = F(X), pour tous X, remplissant la condition X? 0.
Tracer la fonction à = F(X), si à = F(X) est une fonction paire.

3. Dans la fig. comploté à = F(X), pour tout x satisfaisant x ? 0.
Tracer la fonction à = F(X), si à = F(X) est une fonction impaire.

Contrôle mutuel sur glisser.

6. Devoirs : №11.11, 11.21,11.22;

Preuve de la signification géométrique de la propriété de parité.

*** (Affectation de l'option USE).

1. La fonction impaire y \u003d f (x) est définie sur toute la ligne réelle. Pour toute valeur non négative de la variable x, la valeur de cette fonction coïncide avec la valeur de la fonction g( X) = X(X + 1)(X + 3)(X- sept). Trouver la valeur de la fonction h( X) = à X = 3.

7. Résumé