Idées bayésiennes pour les gestionnaires. Une explication simple du théorème bayésien

Page utile ? Enregistrez ou dites à vos amis

Si l'événement UNE ne peut se produire que lorsque l'un des événements qui forment un groupe complet d'événements incompatibles, alors la probabilité de l'événement UNE calculé par la formule

Cette formule s'appelle formule de probabilité totale.

Considérons à nouveau l'ensemble des événements incompatibles, dont les probabilités sont ... Événement UNE ne peut se produire qu'avec n'importe lequel des événements, que nous appellerons hypothèses... Alors par la formule de probabilité totale

Si l'événement UNE s'est produit, alors cela peut changer les probabilités des hypothèses .

Par le théorème de multiplication de probabilité

.

De même, pour d'autres hypothèses

La formule résultante s'appelle formule de Bayes (par la formule bayésienne). Les probabilités des hypothèses sont appelées probabilités postérieures, tandis que - probabilités antérieures.

Exemple. Le magasin a reçu de nouveaux produits de trois entreprises. Le pourcentage de ces produits est le suivant : 20 % - produits de la première société, 30 % - produits de la deuxième société, 50 % - produits de la troisième société ; en outre, 10% des produits de la première entreprise sont de la plus haute qualité, dans la deuxième entreprise - 5% et dans la troisième - 20% des produits de la plus haute qualité. Trouvez la probabilité qu'un nouveau produit acheté accidentellement soit de la plus haute qualité.

Solution. Notons par V un événement consistant en l'achat d'un produit premium, par nous désignons les événements consistant en l'achat de produits appartenant respectivement aux première, deuxième et troisième entreprises.

Vous pouvez appliquer la formule de la probabilité totale, et dans notre notation :

En substituant ces valeurs dans la formule de la probabilité totale, nous obtenons la probabilité souhaitée :

Exemple. L'un des trois tireurs est appelé dans la ligne de mire et tire deux coups. La probabilité de toucher la cible d'un coup pour le premier tireur est de 0,3, pour le second de 0,5; pour le troisième - 0,8. La cible n'est pas touchée. Trouvez la probabilité que les coups aient été tirés par le premier tireur.

Solution. Trois hypothèses sont possibles :

Le premier tireur est appelé sur la ligne de tir,

Un deuxième tireur a été appelé dans la ligne de mire

Un troisième tireur a été appelé dans la ligne de mire.

Puisque l'appel à la ligne de mire de n'importe quel tireur est également possible, alors

À la suite de l'expérience, l'événement B a été observé - après les coups de feu, la cible n'a pas été touchée. Probabilités conditionnelles de cet événement, avec les hypothèses faites, sont égaux à :

en utilisant la formule de Bayes, on trouve la probabilité de l'hypothèse après l'expérience :

Exemple. Sur trois machines automatiques, des pièces du même type sont traitées, qui arrivent après traitement sur un convoyeur commun. La première machine donne 2% de ferraille, la seconde - 7%, la troisième - 10%. La productivité de la première machine est 3 fois supérieure à la productivité de la seconde, et la troisième est 2 fois inférieure à la seconde.

a) Quel est le pourcentage de défauts sur le convoyeur ?

b) Quelles sont les proportions de pièces de chaque machine-outil parmi les pièces défectueuses sur le convoyeur ?

Solution. Prenons une pièce au hasard sur la chaîne de montage et considérons l'événement A - une pièce défectueuse. Il est associé à des hypothèses sur l'endroit où cette pièce a été usinée : - une pièce prise au hasard a été usinée sur la ème machine,.

Probabilités conditionnelles (dans l'énoncé du problème, elles sont données sous forme de pourcentages) :

Les dépendances entre la productivité de la machine signifient ce qui suit :

Et puisque les hypothèses forment un groupe complet, alors.

Après avoir résolu le système d'équations résultant, nous trouvons :.

a) La probabilité totale que la pièce prise au hasard sur la chaîne de montage soit défectueuse.

Qui est Bayes ? et qu'est-ce que cela a à voir avec la gestion? - une question tout à fait juste peut suivre. Pour l'instant, croyez-moi sur parole : c'est très important ! .. et intéressant (du moins pour moi).

Dans quel paradigme la plupart des managers opèrent-ils : si j'observe quelque chose, quelles conclusions puis-je en tirer ? Ce que Bayes enseigne : que doit-il être réellement pour que je puisse observer ce quelque chose ? C'est ainsi que se développent toutes les sciences, et il écrit à ce sujet (je cite de mémoire) : une personne qui n'a pas de théorie en tête va sauter d'une idée à une autre sous l'influence de divers événements(observations). Ce n'est pas pour rien qu'ils disent : il n'y a rien de plus pratique qu'une bonne théorie.

Exemple pratique. Mon subordonné fait une erreur, et mon collègue (le chef d'un autre département) dit qu'il faudrait exercer une influence managériale sur un employé négligent (autrement dit, punir / gronder). Et je sais que cet employé fait 4 à 5 000 opérations du même type par mois, et pendant ce temps, il ne fait pas plus de 10 erreurs. Sentez-vous la différence de paradigme? Mon collègue réagit à l'observation, et j'ai connaissance a priori que l'employé fait un certain nombre d'erreurs, donc une autre n'a pas affecté cette connaissance... Or, si à la fin du mois il s'avère qu'il y a, par exemple, 15 de ces erreurs !.. Cela deviendra une raison pour enquêter sur les raisons du non-respect des normes.

Convaincu de l'importance de l'approche bayésienne ? Intrigué ? J'espère". Et maintenant, une mouche dans la pommade. Malheureusement, les idées de Bayes sont rarement données du premier coup. J'ai été franchement malchanceux, puisque j'ai pris connaissance de ces idées de la littérature populaire, après lecture desquelles de nombreuses questions restaient. Lors de la planification d'écrire une note, j'ai rassemblé tout ce que j'avais précédemment décrit sur Bayes et j'ai également étudié ce qu'ils écrivent sur Internet. Je porte à votre attention ma meilleure hypothèse sur le sujet Introduction à la probabilité bayésienne.

Dérivation du théorème de Bayes

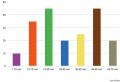
Considérons l'expérience suivante : on nomme n'importe quel nombre se trouvant sur un segment et on le fixe lorsque ce nombre est, par exemple, compris entre 0,1 et 0,4 (Fig. 1a). La probabilité de cet événement est égale au rapport de la longueur du segment sur longueur totale segment, à condition que l'apparition de chiffres sur le segment équiprobable... Mathématiquement, cela peut s'écrire p(0,1 <= X <= 0,4) = 0,3, или кратко R(X) = 0,3, où R- probabilité, X- variable aléatoire dans la plage, X- une variable aléatoire dans la plage. C'est-à-dire que la probabilité de toucher le segment est de 30%.

Riz. 1. Interprétation graphique des probabilités

Considérons maintenant le carré x (Fig. 1b). Disons que nous devons nommer des paires de nombres ( X, oui), dont chacun est supérieur à zéro et inférieur à un. La probabilité que X(le premier nombre) sera dans le segment (zone bleue 1), égal au rapport de l'aire de la zone bleue à l'aire de tout le carré, c'est-à-dire (0,4 - 0,1) * (1 - 0) / (1 * 1) = 0, 3, c'est-à-dire les mêmes 30%. La probabilité que oui est à l'intérieur du segment (zone verte 2) est égal au rapport de la superficie de la zone verte à la superficie de l'ensemble du carré p(0,5 <= y <= 0,7) = 0,2, или кратко R(Oui) = 0,2.

Que peut-on apprendre sur les valeurs en même temps X et oui... Par exemple, quelle est la probabilité qu'en même temps X et oui sont dans les segments donnés correspondants ? Pour ce faire, vous devez calculer le rapport de l'aire de la zone 3 (intersection des rayures vertes et bleues) à l'aire de l'ensemble du carré : p(X, Oui) = (0,4 – 0,1) * (0,7 – 0,5) / (1 * 1) = 0,06.

Disons maintenant que nous voulons savoir quelle est la probabilité que oui est dans l'intervalle si X est déjà dans l'intervalle. C'est, en fait, nous avons un filtre et quand nous appelons des paires ( X, oui), alors nous écartons immédiatement les paires qui ne satisfont pas à la condition de trouver X dans un intervalle donné, puis parmi les paires filtrées on compte celles pour lesquelles oui satisfait notre condition et nous considérons la probabilité comme le rapport du nombre de paires pour lesquelles oui se situe dans le segment susmentionné au nombre total de paires filtrées (c'est-à-dire pour lesquelles X se trouve dans le segment). On peut écrire cette probabilité sous la forme p(Oui|X à X frapper la gamme. " Évidemment, cette probabilité est égale au rapport de l'aire de la zone 3 à l'aire de la zone bleue 1. L'aire de la zone 3 est (0,4 - 0,1) * (0,7 - 0,5) = 0,06, et la zone de la zone bleue 1 (0,4 - 0,1) * (1 - 0) = 0,3, alors leur rapport est de 0,06 / 0,3 = 0,2. En d'autres termes, la probabilité de trouver oui sur un segment à condition que X appartient au segment p(Oui|X) = 0,2.

Dans le paragraphe précédent, nous avons en fait formulé l'identité : p(Oui|X) = p(X, Oui) / p ( X). Il se lit comme suit : « la probabilité de toucher à dans la gamme, à condition que X atteint la portée, est égal au rapport de la probabilité d'un coup simultané X dans la gamme et à dans la gamme, à la probabilité de toucher X dans la gamme ".

Par analogie, considérons la probabilité p(X|Oui). Nous appelons des paires ( X, oui) et filtrer ceux pour lesquels oui est compris entre 0,5 et 0,7, alors la probabilité que X est dans le segment à condition que oui appartient au segment est égal au rapport de la surface de la zone 3 sur la surface de la zone verte 2 : p(X|Oui) = p(X, Oui) / p(Oui).

Notez que les probabilités p(X, Oui) et p(Y, X) sont égaux, et les deux sont égaux au rapport de l'aire de la zone 3 à l'aire du carré entier, mais les probabilités p(Oui|X) et p(X|Oui) inégal; tandis que la probabilité p(Oui|X) est égal au rapport de l'aire de la région 3 à la région 1, et p(X|Oui) - de la région 3 à la région 2. Notez également que p(X, Oui) est souvent noté p(X&Oui).

Nous avons donc introduit deux définitions : p(Oui|X) = p(X, Oui) / p ( X) et p(X|Oui) = p(X, Oui) / p(Oui)

Réécrivons ces égalités comme : p(X, Oui) = p(Oui|X) * p ( X) et p(X, Oui) = p(X|Oui) * p(Oui)

Puisque les membres de gauche sont égaux, les membres de droite sont également égaux : p(Oui|X) * p ( X) = p(X|Oui) * p(Oui)

Ou nous pouvons réécrire la dernière égalité sous la forme :

C'est le théorème de Bayes !

Est-il possible que des transformations aussi simples (presque tautologiques) donnent lieu au grand théorème !? Ne sautez pas aux conclusions. Parlons encore de ce que nous avons. Il y avait une probabilité initiale (antérieure) R(X), le fait que la variable aléatoire X uniformément répartie sur un segment se situe dans la plage X... Quelque chose est arrivé Oui, ce qui nous a permis d'obtenir la probabilité a posteriori de la même variable aléatoire X: R(X | Y), et cette probabilité diffère de R(X) par le coefficient. Événement Oui appelé preuve, plus ou moins confirmant ou réfutant X... Ce rapport est parfois appelé pouvoir de preuve... Plus la preuve est puissante, plus le fait d'observer Y modifie la probabilité a priori, plus la probabilité a posteriori diffère de la probabilité a priori. Si la preuve est faible, la probabilité postérieure est presque égale à la probabilité antérieure.

Formule de Bayes pour les variables aléatoires discrètes

Dans la section précédente, nous avons dérivé la formule de Bayes pour les variables aléatoires continues x et y définies sur un segment. Prenons un exemple avec des variables aléatoires discrètes, chacune prenant deux valeurs possibles. Au cours des examens médicaux de routine, il a été constaté qu'à l'âge de quarante ans, 1% des femmes souffrent d'un cancer du sein. 80% des femmes atteintes de cancer reçoivent des mammographies positives. 9,6 % des femmes en bonne santé obtiennent également des résultats de mammographie positifs. Au cours de l'examen, une femme de ce groupe d'âge a reçu un résultat de mammographie positif. Quelle est la probabilité qu'elle ait réellement un cancer du sein ?

La ligne de raisonnement / calculs est la suivante. Sur 1 % des patientes atteintes de cancer, la mammographie donnera 80 % de résultats positifs = 1 % * 80 % = 0,8 %. Sur 99% des femmes en bonne santé, la mammographie donnera 9,6% de résultats positifs = 99% * 9,6% = 9,504%. Au total, sur 10,304% (9,504% + 0,8%) avec des résultats de mammographie positifs, seulement 0,8% des patientes, et les 9,504% restants sont en bonne santé. Ainsi, la probabilité qu'une femme ait un cancer avec une mammographie positive est de 0,8% / 10,304 % = 7,764%. Pensiez-vous à 80 % environ ?

Dans notre exemple, la formule de Bayes prend la forme suivante :

Rappelons le sens « physique » de cette formule. X- une variable aléatoire (diagnostic), prenant des valeurs : X 1- malade et X 2- sain; Oui- variable aléatoire (résultat de la mesure - mammographie), prenant les valeurs : Oui 1- un résultat positif et Oui 2- résultat négatif ; p (x 1)- la probabilité de maladie avant mammographie (probabilité préalable), égale à 1% ; R(Oui 1 |X 1 ) - la probabilité d'un résultat positif si le patient est malade (probabilité conditionnelle, puisqu'elle doit être précisée dans les conditions du problème), égale à 80% ; R(Oui 1 |X 2 ) – la probabilité d'un résultat positif si le patient est en bonne santé (également une probabilité conditionnelle), égale à 9,6 % ; p (X 2)- la probabilité que la patiente soit en bonne santé avant la mammographie (probabilité préalable) égale à 99% ; p (X 1|Oui 1 ) – la probabilité que la patiente soit malade, sous réserve d'un résultat mammographique positif (probabilité postérieure).

On voit que la probabilité a posteriori (ce que l'on cherche) est proportionnelle à la probabilité a priori (initiale) avec un coefficient un peu plus complexe ... Permettez-moi de souligner à nouveau. À mon avis, c'est un aspect fondamental de l'approche bayésienne. La mesure ( Oui) a ajouté un certain nombre d'informations à celles initialement disponibles (a priori), qui ont affiné notre connaissance de l'objet.

Exemples de

Essayez de résoudre plusieurs problèmes pour consolider le matériau recouvert.

Exemple 1. Il y a 3 urnes ; dans les 3 premières boules blanches et 1 noire ; dans le second - 2 boules blanches et 3 noires; dans le troisième - 3 boules blanches. Quelqu'un vient au hasard dans l'une des urnes et en sort 1 boule. Cette boule s'est avérée être blanche. Trouvez les probabilités postérieures que la balle soit sortie de la 1ère, 2ème, 3ème urne.

Solution. Nous avons trois hypothèses : N 1 = (la première urne est sélectionnée), N 2 = (la deuxième urne est sélectionnée), N 3 = (la troisième urne est sélectionnée). L'urne étant choisie au hasard, les probabilités a priori des hypothèses sont égales : P (H 1) = P (H 2) = P (H 3) = 1/3.

À la suite de l'expérience, l'événement A = est apparu (une boule blanche a été retirée de l'urne sélectionnée). Probabilités conditionnelles de l'événement A sous les hypothèses H 1, H 2, H 3 : P (A | H 1) = 3/4, P (A | H 2) = 2/5, P (A | H 3) = 1. Par exemple, la première égalité se lit comme suit : "la probabilité de sortir la boule blanche si la première urne est sélectionnée est de 3/4 (puisqu'il y a 4 boules dans la première urne, et 3 d'entre elles sont blanches)."

En appliquant la formule de Bayes, on trouve les probabilités postérieures des hypothèses :

Ainsi, à la lumière des informations sur la survenance de l'événement A, les probabilités des hypothèses ont changé : l'hypothèse la plus probable est devenue l'hypothèse H 3, la moins probable - l'hypothèse H 2.

Exemple 2. Deux tireurs indépendamment l'un de l'autre tirent sur la même cible, chacun tirant un coup. La probabilité de toucher la cible pour le premier tireur est de 0,8, pour le second de 0,4. Après le tir, un trou a été trouvé dans la cible. Trouvez la probabilité que ce trou appartienne au premier tireur (Nous rejetons le résultat (les deux trous ont coïncidé) comme étant négligeable).

Solution. Avant l'expérience, les hypothèses suivantes sont possibles : H 1 = (ni la première ni la deuxième flèches ne toucheront), H 2 = (les deux flèches toucheront), H 3 - (le premier tireur touchera, et le second ne touchera pas) ), H 4 = (le premier tireur ne touchera pas, et le second touchera). Probabilités a priori des hypothèses :

P(H1) = 0,2 * 0,6 = 0,12 ; P(H2) = 0,8 * 0,4 = 0,32 ; P(H3) = 0,8 * 0,6 = 0,48; P(H4) = 0,2 * 0,4 = 0,08.

Les probabilités conditionnelles de l'événement observé A = (il y a un trou dans la cible) sous ces hypothèses sont : P (A | H 1) = P (A | H 2) = 0 ; P (A | H 3) = P (A | H 4) = 1

Après l'expérience, les hypothèses H 1 et H 2 deviennent impossibles, et les probabilités postérieures des hypothèses H 3 et H 4 selon la formule bayésienne seront :

anti-spam bayésien

La formule de Bayes a trouvé une large application dans le développement de filtres anti-spam. Supposons que vous souhaitiez former un ordinateur pour détecter lequel des e-mails est du spam. Nous partirons d'un dictionnaire et de phrases utilisant des estimations bayésiennes. Créons d'abord l'espace d'hypothèse. Supposons que nous ayons 2 hypothèses pour n'importe quelle lettre : H A est un spam, H B n'est pas un spam, mais une lettre normale, nécessaire.

Tout d'abord, nous allons "former" notre futur système anti-spam. Prenons toutes les lettres que nous avons et divisons-les en deux "tas" de 10 lettres chacun. Mettons les messages de spam dans l'un et appelons-le tas H A, dans l'autre - la correspondance nécessaire et appelons-le tas H B. Voyons maintenant : quels mots et expressions se trouvent dans les spams et les e-mails nécessaires et à quelle fréquence ? Appelons ces mots et expressions preuves et désignons-les E 1, E 2 ... Il s'avère que les mots courants (par exemple, les mots « comment », « votre » dans les tas HA et HB se produisent avec approximativement le même la fréquence. Ainsi, la présence de ces mots dans une lettre ne nous dit rien sur le tas auquel se référer (faible évidence). Attribuons à ces mots une valeur neutre pour la probabilité de "spam", disons 0,5.

Laissez l'expression "français familier" apparaître dans seulement 10 e-mails, et plus souvent dans les e-mails de spam (par exemple, dans 7 e-mails de spam sur 10) que dans les e-mails nécessaires (dans 3 sur 10). Mettons cette phrase pour le spam avec un score plus élevé de 7/10, et pour les e-mails normaux, un score inférieur : 3/10. A l'inverse, il s'est avéré que le mot « copain » était plus courant en lettres normales (6 sur 10). Et donc nous avons reçu une courte lettre: "Copain! Comment est ton anglais parlé ?"... Essayons d'évaluer son "spam". Nous mettons les estimations générales P (H A), P (H B) d'une lettre appartenant à chaque tas, en utilisant une formule de Bayes quelque peu simplifiée et nos estimations approximatives :

P (H A) = A / (A + B), où A = p a1 * p a2 *… * p an, B = p b1 * p b2 *… * p b n = (1 - p a1) * (1 - p a2) *… * (1 - p an).

Tableau 1. Score d'écriture bayésienne simplifié (et incomplet)

Ainsi, notre lettre hypothétique a reçu une estimation de la probabilité d'appartenance, en mettant l'accent sur le « spam ». Pouvons-nous décider de jeter la lettre dans l'une des piles ? Fixons les seuils de prise de décision :

• On supposera qu'une lettre appartient au tas H i si P (H i) T.
• Une lettre n'appartient pas au tas si P (H i) L.
• Si L P (H i) T, aucune décision ne peut être prise.

Vous pouvez prendre T = 0,95 et L = 0,05. Puisque pour la lettre en question et 0,05< P(H A) < 0,95, и 0,05 < P(H В) < 0,95, то мы не сможем принять решение, куда отнести данное письмо: к спаму (H A) или к нужным письмам (H B). Можно ли улучшить оценку, используя больше информации?

Oui. Calculons le score de chaque élément de preuve d'une manière différente, comme l'a suggéré Bayes. Laisser:

F a est le nombre total de messages de spam ;

F ai est le nombre de lettres avec un certificat je dans un tas de spam ;

F b est le nombre total de lettres requises ;

F bi est le nombre de lettres avec un certificat je dans un tas de lettres nécessaires (pertinentes).

Alors : p ai = F ai / F a, p bi = F bi / F b. P (H A) = A / (A + B), P (H B) = B / (A + B), où A = p a1 * p a2 *… * p an, B = p b1 * p b2 *… * p b n

Faites attention - les évaluations des mots p ai et p bi sont devenues objectives et peuvent être calculées sans intervention humaine.

Tableau 2. Une estimation bayésienne plus précise (mais incomplète) basée sur les signes disponibles d'une lettre

Nous avons obtenu un résultat assez précis - avec une grande marge de probabilité, la lettre peut être attribuée aux lettres nécessaires, puisque P (H B) = 0,997> T = 0,95. Pourquoi le résultat a-t-il changé ? Parce que nous avons utilisé plus d'informations - nous avons pris en compte le nombre de lettres dans chacun des tas et, en passant, avons déterminé les estimations p ai et p bi beaucoup plus correctement. Nous les avons définis comme Bayes lui-même en calculant des probabilités conditionnelles. En d'autres termes, p a3 est la probabilité que le mot "ami" apparaisse dans la lettre, à condition que cette lettre appartienne déjà au tas de spams H A. Le résultat ne s'est pas fait attendre - il semble que nous puissions prendre une décision avec plus de certitude.

Bayes contre fraude en entreprise

Une application intéressante de l'approche bayésienne a été décrite par MAGNUS8.

Dans mon projet actuel (SI pour détecter la fraude dans une entreprise manufacturière), la formule bayésienne est utilisée pour déterminer la probabilité de fraude (fraude) en présence/absence de plusieurs faits qui soutiennent indirectement l'hypothèse de la possibilité de fraude. L'algorithme est autodidacte (avec retour d'informations), c'est-à-dire recalcule ses coefficients (probabilités conditionnelles) en cas de confirmation effective ou de non-confirmation de la fraude lors du contrôle du service de sécurité économique.

Il vaut probablement la peine de dire que de telles méthodes dans la conception d'algorithmes nécessitent une culture mathématique suffisamment élevée du développeur, car la moindre erreur dans la dérivation et/ou la mise en œuvre des formules de calcul annulera et discréditera l'ensemble de la méthode. Les méthodes probabilistes pèchent en particulier avec cela, car la pensée humaine n'est pas adaptée pour travailler avec des catégories probabilistes et, par conséquent, il n'y a pas de « visualisation » et de compréhension de la « signification physique » des paramètres probabilistes intermédiaires et finaux. Cette compréhension ne concerne que les concepts de base de la théorie des probabilités, et il vous suffit ensuite de combiner et de déduire très soigneusement des choses complexes selon les lois de la théorie des probabilités - le bon sens pour les objets composites ne sera plus utile. Ceci, en particulier, est associé à des batailles méthodologiques assez sérieuses qui se déroulent dans les pages de livres modernes sur la philosophie des probabilités, ainsi qu'à un grand nombre de sophismes, de paradoxes et de problèmes de curiosité sur ce sujet.

Une autre nuance à laquelle j'ai dû faire face - malheureusement, presque tout ce qui est plus ou moins UTILE EN PRATIQUE sur ce sujet est écrit en anglais. Dans les sources en russe, fondamentalement seulement une théorie bien connue avec des exemples de démonstration uniquement pour les cas les plus primitifs.

Je suis tout à fait d'accord avec la dernière remarque. Par exemple, Google, en essayant de trouver quelque chose comme "des livres de probabilité bayésiens", n'a rien donné d'intelligible. Certes, il a dit que le livre avec les statistiques bayésiennes était interdit en Chine. (Le professeur de statistiques Andrew Gelman a déclaré sur un blog de l'Université de Columbia que son livre Analyser les données à l'aide de la régression et des modèles hiérarchiques / superposés avait été interdit de publication en Chine. texte. ») Je me demande si une raison similaire a conduit à l'absence de livres sur les probabilités bayésiennes en Chine. Russie?

Conservatisme dans le processus de traitement de l'information humaine

Les probabilités déterminent le degré d'incertitude. La probabilité, à la fois selon Bayes et notre intuition, est simplement un nombre entre zéro et ce qui représente le degré auquel une personne quelque peu idéalisée pense que la déclaration est vraie. La raison pour laquelle une personne est quelque peu idéalisée est que la somme de ses probabilités pour deux événements mutuellement exclusifs doit être égale à sa probabilité que l'un de ces événements se produise. La propriété d'additivité a de telles conséquences que peu de personnes réelles peuvent les égaler toutes.

Le théorème de Bayes est une conséquence triviale de la propriété d'additivité, indiscutable et cohérente pour tous les tenants de la probabilité, bayésienne et autres. Une façon de l'écrire est la suivante. Si P (H A | D) est la probabilité subséquente que l'hypothèse A soit après qu'une valeur donnée de D ait été observée, P (H A) est sa probabilité antérieure avant qu'une valeur donnée de D ne soit observée, P (D | H A ) est la probabilité qu'une quantité donnée D sera observée, si HA est vrai, et P (D) est la probabilité inconditionnelle d'une quantité donnée D, alors

(1) P (H A | D) = P (D | H A) * P (H A) / P (D)

P (D) est mieux considéré comme une constante de normalisation qui fait que les probabilités postérieures s'additionnent à un sur l'ensemble exhaustif d'hypothèses mutuellement exclusives considérées. S'il doit être calculé, cela peut être comme ceci :

Mais le plus souvent P (D) est éliminé plutôt que compté. Un moyen pratique de le corriger est de transformer le théorème de Bayes sous la forme d'un rapport probabilité-chance.

Considérons une autre hypothèse, H B, qui est mutuellement exclusive de H A, et changeons d'avis à ce sujet en fonction de la même quantité donnée qui a changé d'avis à propos de H A. Le théorème de Bayes dit que

(2) P (H B | D) = P (D | H B) * P (H B) / P (D)

Divisez maintenant l'équation 1 par l'équation 2 ; le résultat sera comme ça :

où 1 sont les cotes postérieures en faveur de HA à H B, Ω 0 sont les cotes antérieures et L est le montant connu des statisticiens en tant que rapport de probabilité. L'équation 3 est la même version correspondante du théorème de Bayes que l'équation 1, et est souvent beaucoup plus utile, en particulier pour les expériences impliquant des hypothèses. Les partisans de Bayes soutiennent que le théorème de Bayes est une règle empirique formellement optimale sur la façon de réviser les opinions à la lumière de nouvelles données.

Nous sommes intéressés à comparer le comportement idéal défini par le théorème de Bayes avec le comportement réel des personnes. Pour vous donner une idée de ce que cela signifie, essayons une expérience avec vous en tant que sujet. Ce sac contient 1000 jetons de poker. J'ai deux de ces sacs, un avec 700 jetons rouges et 300 jetons bleus, et l'autre avec 300 jetons rouges et 700 jetons bleus. J'ai lancé une pièce pour déterminer laquelle utiliser. Donc, si nos opinions sont les mêmes, votre chance actuelle d'obtenir un sac avec plus de jetons rouges est de 0,5. Maintenant, vous sélectionnez au hasard une sélection avec un retour après chaque jeton. En 12 jetons, vous obtenez 8 rouges et 4 bleus. Maintenant, d'après tout ce que vous savez, quelle est la probabilité que le sac tombe, où sont les plus rouges ? Il est clair qu'il est supérieur à 0,5. S'il vous plaît, ne poursuivez pas votre lecture avant d'avoir écrit votre note.

Si vous êtes comme un sujet de test typique, votre score se situe entre 0,7 et 0,8. Si nous faisions le calcul approprié, cependant, la réponse serait 0,97. En effet, il est très rare qu'une personne à qui on n'a pas montré auparavant l'influence du conservatisme arrive à une évaluation aussi élevée, même s'il était familier avec le théorème de Bayes.

Si la part de chips rouges dans le sac est R, alors la probabilité d'obtenir r chips rouges et ( n-r) bleu dans méchantillons avec retour - p r (1–p)n–r... Ainsi, dans une expérience typique de sac et de jeton de poker, si NUNE signifie que la part des jetons rouges est p Un et NB- signifie que la part est RB, alors le rapport de probabilité est :

Lors de l'application de la formule de Bayes, seules les probabilités de l'observation réelle doivent être prises en compte, pas les probabilités d'autres observations qu'il aurait pu faire mais ne l'ont pas fait. Ce principe a de larges implications pour toutes les applications statistiques et non statistiques du théorème de Bayes ; c'est l'outil technique le plus important pour la pensée bayésienne.

Révolution bayésienne

Vos amis et collègues parlent de quelque chose appelé théorème bayésien ou règle bayésienne, ou quelque chose appelé pensée bayésienne. Cela les intéresse vraiment, alors vous allez en ligne et trouvez une page sur le théorème de Bayes et... C'est une équation. Et c'est tout... Pourquoi un concept mathématique suscite-t-il un tel engouement dans les esprits ? Quel genre de « révolution bayésienne » est en train de se produire parmi les scientifiques, et l'on soutient que même l'approche expérimentale elle-même peut être décrite comme son cas particulier ? Quel est le secret que connaissent les Bayesiens ? Quel genre de lumière voient-ils ?

La révolution bayésienne de la science ne s'est pas produite parce que de plus en plus de scientifiques cognitifs ont soudainement commencé à remarquer que les phénomènes mentaux ont une structure bayésienne ; pas parce que les scientifiques de tous les domaines ont commencé à utiliser des méthodes bayésiennes ; mais parce que la science elle-même est un cas particulier du théorème de Bayes ; les preuves expérimentales sont des preuves bayésiennes. Les révolutionnaires bayésiens soutiennent que lorsque vous effectuez une expérience et recevez des preuves qui "confirment" ou "réfutent" votre théorie, cette confirmation ou réfutation suit les règles bayésiennes. Par exemple, vous devez tenir compte non seulement du fait que votre théorie peut expliquer un phénomène, mais qu'il existe d'autres explications possibles qui peuvent également prédire ce phénomène.

Auparavant, la philosophie des sciences la plus populaire était une ancienne philosophie qui a été remplacée par la révolution bayésienne. L'idée de Karl Popper selon laquelle les théories peuvent être complètement falsifiées, mais ne peuvent jamais être entièrement confirmées, est un autre cas particulier des règles bayésiennes ; si p (X | A) 1 - si la théorie fait des prédictions correctes, alors l'observation ~ X fausse très fortement A. En revanche, si p (X | A) 1 et on observe X, cela ne confirme pas fortement la théorie; peut-être une autre condition B telle que p (X | B) 1, et sous laquelle l'observation X ne témoigne pas en faveur de A mais témoigne en faveur de B. Pour observer X confirmer définitivement A, il faudrait connaître le tort que p (X | A) 1, et que p (X | ~ A) 0, que nous ne pouvons pas connaître, car nous ne pouvons pas considérer toutes les explications alternatives possibles. Par exemple, lorsque la théorie de la relativité générale d'Einstein a dépassé la théorie de la gravité bien étayée de Newton, elle a fait de toutes les prédictions de Newton un cas particulier des prédictions d'Einstein.

De même, la déclaration de Popper selon laquelle une idée doit être falsifiée peut être interprétée comme une manifestation de la règle bayésienne de préservation de la probabilité ; si le résultat X est une preuve positive de la théorie, alors le résultat ~ X doit réfuter la théorie dans une certaine mesure. Si vous essayez d'interpréter à la fois X et ~ X comme des théories « de soutien », les règles bayésiennes disent que c'est impossible ! Pour augmenter la probabilité d'une théorie, vous devez la soumettre à des tests qui pourraient potentiellement réduire sa probabilité ; ce n'est pas seulement une règle pour repérer les charlatans en science, mais un corollaire du théorème de probabilité bayésien. D'un autre côté, l'idée de Popper selon laquelle seule la falsification est nécessaire et aucune confirmation n'est nécessaire est incorrecte. Le théorème de Bayes montre que la falsification est une preuve très forte par rapport à la confirmation, mais la falsification est toujours de nature probabiliste ; elle n'est pas régie par des règles fondamentalement différentes et ne diffère pas en cela de la confirmation, comme le soutient Popper.

Ainsi, nous constatons que de nombreux phénomènes dans les sciences cognitives, plus les méthodes statistiques utilisées par les scientifiques, plus la méthode scientifique elle-même, sont tous des cas particuliers du théorème de Bayes. C'est ce qu'est la révolution bayésienne.

Bienvenue dans le complot bayésien !

Littérature de probabilité bayésienne

2. De nombreuses applications différentes de Bayes sont décrites par le lauréat du prix Nobel d'économie Kahneman (avec des amis) dans un livre merveilleux. Dans mon seul résumé de ce très gros livre, j'ai compté 27 mentions du nom du prêtre presbytérien. Un minimum de formules. (.. J'ai beaucoup aimé. C'est vrai, compliqué, beaucoup de maths (et où sans), mais des chapitres individuels (par exemple, chapitre 4. Information), clairement sur le sujet. Je conseille à tout le monde. Même si les maths sont difficiles pour vous, lisez toute la ligne en sautant les maths et en pêchant les bons grains...

14. (ajout du 15 janvier 2017), un chapitre du livre de Tony Crilly. 50 idées à connaître. Mathématiques.

Le physicien lauréat du prix Nobel Richard Feynman, parlant d'un philosophe avec une grande suffisance, a dit un jour : « Ce n'est pas la philosophie en tant que science qui m'ennuie, mais la pompe qui a été créée autour d'elle. Si seulement les philosophes pouvaient rire d'eux-mêmes ! Si seulement ils pouvaient dire : "Je dis que c'est comme ça, mais Von Leipzig pensait que c'était différent, mais il comprend aussi quelque chose à ce sujet." Si seulement ils n'oubliaient pas d'expliquer que ce n'était que leur .

Que leurs probabilités et les probabilités conditionnelles correspondantes soient connues. Alors la probabilité d'occurrence de l'événement est égale à :

Cette formule s'appelle formules de probabilité totale... Dans les manuels, il est formulé par un théorème dont la démonstration est élémentaire : d'après algèbre des événements, (l'événement s'est produit et ou un événement s'est produit et après il est venu l'événement ou un événement s'est produit et après il est venu l'événement ou …. ou un événement s'est produit et après l'événement)... Puisque les hypothèses incompatible, et l'événement est dépendant, alors par théorème d'addition pour les probabilités d'événements incohérents (premier pas) et théorème de multiplication pour les probabilités d'événements dépendants (deuxième étape):

Probablement, beaucoup ont un pressentiment du contenu du premier exemple =)

Partout où vous crachez - partout une urne :

Problème 1

Il y a trois urnes identiques. Dans la première urne, il y a 4 boules blanches et 7 noires, dans la seconde - uniquement des boules blanches et dans la troisième - uniquement des boules noires. Une urne est choisie au hasard et une boule en est tirée au hasard. Quelle est la probabilité que cette boule soit noire ?

Solution: considérez l'événement - une boule noire sera extraite d'une urne choisie au hasard. Cet événement peut survenir à la suite de la mise en œuvre de l'une des hypothèses suivantes :
- la 1ère urne sera sélectionnée ;
- la 2ème urne sera sélectionnée ;
- la 3ème urne sera sélectionnée.

Puisque l'urne est choisie au hasard, le choix de l'une des trois urnes tout aussi possible, Par conséquent:

Veuillez noter que les hypothèses énumérées forment groupe complet d'événements, c'est-à-dire que par condition, une boule noire ne peut apparaître que de ces urnes, et par exemple, ne pas s'envoler d'un billard. Faisons un simple contrôle intermédiaire :
, OK, passons à autre chose :

La première urne contient 4 blanches + 7 noires = 11 boules, chacune définition classique:
- la probabilité d'extraire une boule noire fourni que la 1ère urne sera sélectionnée.

Il n'y a que des boules blanches dans la deuxième urne, donc si choisi l'apparition de la boule noire devient impossible: .

Et, enfin, dans la troisième urne il n'y a que des boules noires, ce qui signifie que la probabilite conditionnelle extraire la boule noire sera (événement valide).

- la probabilité qu'une boule noire soit retirée d'une urne choisie au hasard.

Réponse:

L'exemple analysé suggère à nouveau à quel point il est important de PLAIRE DANS UNE CONDITION. Reprenons les mêmes problèmes avec les urnes et les boules - avec leur similitude externe, les méthodes de solution peuvent être complètement différentes: quelque part il suffit d'appliquer définition classique de la probabilité, événements quelque part indépendant, quelque part dépendant, mais quelque part on parle d'hypothèses. Dans le même temps, il n'y a pas de critère formel clair pour choisir un chemin de solution - vous devez presque toujours y réfléchir. Comment améliorer vos qualifications? On décide, on décide et on décide encore !

Tâche 2

Il y a 5 fusils de précision différente dans le pas de tir. Les probabilités de toucher la cible pour un tireur donné sont respectivement égales à 0,5 ; 0,55 ; 0,7 ; 0,75 et 0,4. Quelle est la probabilité de toucher une cible si le tireur tire un coup avec une carabine choisie au hasard ?

Une solution courte et une réponse à la fin du tutoriel.

Dans la plupart des problèmes d'actualité, les hypothèses ne sont bien sûr pas également probables :

Problème 3

Il y a 5 fusils dans la pyramide, dont trois sont équipés d'une lunette de visée. La probabilité que le tireur atteigne la cible lorsqu'il tire avec une carabine à lunette est de 0,95 ; pour un fusil sans lunette de visée, cette probabilité est de 0,7. Trouvez la probabilité que la cible soit touchée si le tireur tire un coup avec un fusil pris au hasard.

Solution: dans ce problème, le nombre de fusils est exactement le même que dans le précédent, mais il n'y a que deux hypothèses :
- le tireur choisit une carabine à lunette de visée ;
- le tireur choisit une carabine sans lunette de visée.
Par définition classique de la probabilité: .
Contrôler:

Considérez l'événement : - Le tireur atteint la cible avec un fusil pris au hasard.
Par condition : .

D'après la formule de probabilité totale :

Réponse: 0,85

En pratique, une formalisation abrégée de la tâche, que vous connaissez aussi, est tout à fait acceptable :

Solution: selon la définition classique : - la probabilité de choisir respectivement une carabine avec et sans viseur optique.

Par état, - la probabilité de toucher la cible avec les types de fusils correspondants.

D'après la formule de probabilité totale :
- la probabilité que le tireur atteigne la cible avec un fusil choisi au hasard.

Réponse: 0,85

La tâche suivante pour une solution indépendante :

Problème 4

Le moteur fonctionne selon trois modes : normal, forcé et ralenti. En mode veille, la probabilité de sa défaillance est de 0,05, en fonctionnement normal de 0,1 et en mode forcé de 0,7. 70 % du temps, le moteur tourne en mode normal et 20 % en mode forcé. Quelle est la probabilité d'une panne de moteur pendant le fonctionnement?

Juste au cas où, permettez-moi de vous le rappeler - pour obtenir les valeurs des probabilités, les pourcentages doivent être divisés par 100. Soyez très prudent ! D'après mes observations, les conditions de problèmes pour la formule de probabilité totale sont souvent tentées de se confondre ; et j'ai spécialement sélectionné un tel exemple. Je vais vous dire un secret - je me suis presque perdu moi-même =)

Solution à la fin de la leçon (cadrée de manière courte)

Problèmes de formule bayésienne

Le matériel est étroitement lié au contenu du paragraphe précédent. Laisser l'événement se produire à la suite de la mise en œuvre de l'une des hypothèses ... Comment déterminer la probabilité que telle ou telle hypothèse ait eu lieu ?

Fourni cet événement déjà arrivé, probabilités d'hypothèses surfait selon les formules qui ont reçu le patronyme du prêtre anglais Thomas Bayes :

- la vraisemblance de la réalisation de l'hypothèse ;
- la vraisemblance de la réalisation de l'hypothèse ;
…
- la probabilité que l'hypothèse ait eu lieu.

À première vue, cela semble une absurdité totale - pourquoi recalculer les probabilités des hypothèses, si elles sont déjà connues ? Mais en fait, il y a une différence :

- ce a priori(estimé avant de tests) probabilités.

- ce a postériori(estimé après tests) les probabilités des mêmes hypothèses, recalculées en relation avec des "circonstances nouvellement découvertes" - en tenant compte du fait que l'événement s'est authentiquement produit.

Regardons cette différence avec un exemple spécifique :

Problème 5

L'entrepôt a reçu 2 lots de produits : le premier - 4000 pièces, le second - 6000 pièces. Le pourcentage moyen d'articles non standard dans le premier lot est de 20% et dans le second de 10%. Le produit pris au hasard dans l'entrepôt s'est avéré être standard. Trouvez la probabilité que ce soit : a) du premier lot, b) du deuxième lot.

Première partie solutions consiste à utiliser la formule de la probabilité totale. En d'autres termes, les calculs sont effectués en supposant que le test pas encore produit et événement "Le produit s'est avéré être standard" jusqu'à ce qu'il vienne.

Considérons deux hypothèses :
- le produit pris au hasard sera du 1er lot ;
- le produit pris au hasard sera du 2ème lot.

Total : 4000 + 6000 = 10000 articles en stock. Selon la définition classique :
.

Contrôler:

Considérons un événement dépendant : - un article pris au hasard dans un entrepôt sera la norme.

Dans le premier lot, 100 % - 20 % = 80 % de produits standards, donc : fourni qu'il appartient à la 1ère partie.

De même, dans le deuxième lot, 100 % - 10 % = 90 % de produits standards et - la probabilité que le produit pris au hasard dans l'entrepôt soit standard fourni qu'il appartient à la 2e partie.

D'après la formule de probabilité totale :
- la probabilité que le produit pris au hasard dans l'entrepôt soit standard.

Deuxième partie. Que le produit pris au hasard dans l'entrepôt s'avère être standard. Cette phrase est directement énoncée dans la condition, et elle indique le fait que l'événement arrivé.

D'après les formules de Bayes :

a) est la probabilité que le produit standard sélectionné appartienne au 1er lot ;

b) - la probabilité que le produit standard sélectionné appartienne au 2ème lot.

Après réévaluation des hypothèses, bien sûr, se forment encore groupe complet:
(examen;-))

Réponse:

Ivan Vasilievich nous aidera à comprendre le sens de la réévaluation des hypothèses, qui a de nouveau changé de profession et est devenu directeur de l'usine. Il sait qu'aujourd'hui le 1er atelier a expédié 4 000 articles à l'entrepôt, et le 2e atelier - 6 000 articles, et il vient s'en assurer. Supposons que tous les produits soient du même type et se trouvent dans un seul conteneur. Naturellement, Ivan Vasilyevich a calculé au préalable que le produit, qu'il extraira maintenant pour inspection, sera très probablement produit par le 1er atelier et avec la probabilité - par le second. Mais une fois que l'article sélectionné est standard, il s'exclame : « Quel boulon cool ! - il a plutôt été libéré par la 2ème boutique." Ainsi, la probabilité de la deuxième hypothèse est surestimée pour le mieux, et la probabilité de la première hypothèse est sous-estimée :. Et cette réévaluation n'est pas infondée - après tout, le 2ème atelier a non seulement produit plus de produits, mais fonctionne également 2 fois mieux !

Pure subjectivité, dites-vous ? En partie - oui d'ailleurs, Bayes lui-même a interprété a postériori probabilités comme Niveau de confiance... Cependant, tout n'est pas si simple - il y a un grain objectif dans l'approche bayésienne. Après tout, la probabilité que le produit soit standard (0,8 et 0,9 pour les 1er et 2e ateliers, respectivement) ce préliminaire(a priori) et moyenne estimations. Mais, philosophiquement parlant, tout coule, tout change, y compris les probabilités. Il est possible que au moment de la recherche 2ème atelier plus réussi a augmenté le pourcentage de produits standards (et/ou le 1er atelier réduit), et si vous vérifiez une plus grande quantité ou tous les 10 000 articles en stock, les valeurs surestimées se révéleront beaucoup plus proches de la vérité.

Soit dit en passant, si Ivan Vasilyevich extrait une pièce non standard, alors au contraire - il "suspectera" plus le 1er magasin et moins - le second. Je vous propose de vous en assurer vous-même :

Problème 6

L'entrepôt a reçu 2 lots de produits : le premier - 4000 pièces, le second - 6000 pièces. Le pourcentage moyen d'articles non standard dans le premier lot est de 20%, dans le second - 10%. Le produit pris au hasard dans l'entrepôt s'est avéré être ne pas la norme. Trouvez la probabilité que ce soit : a) du premier lot, b) du deuxième lot.

La condition se distingue par deux lettres, que j'ai surlignées en gras. Le problème peut être résolu à partir de zéro, ou vous pouvez utiliser les résultats des calculs précédents. Dans l'exemple, j'ai réalisé une solution complète, mais pour qu'il n'y ait pas de chevauchement formel avec la tâche n°5, l'événement "Le produit pris au hasard de l'entrepôt sera non standard" désigné par.

Le schéma bayésien de surestimation des probabilités est omniprésent et divers fraudeurs l'exploitent également activement. Considérez la société par actions à trois lettres qui est devenue un nom familier, qui attire les dépôts de la population, les investirait prétendument quelque part, verse régulièrement des dividendes, etc. Que ce passe-t-il? Jour après jour, mois après mois, et de plus en plus de faits nouveaux, véhiculés par la publicité et le bouche à oreille, ne font qu'augmenter le niveau de confiance dans la pyramide financière. (Réévaluation bayésienne post hoc due aux événements passés !)... Autrement dit, aux yeux des déposants, il y a une augmentation constante de la probabilité que "C'est un bureau sérieux"; alors que la probabilité de l'hypothèse inverse est ("Ce sont les prochains escrocs"), bien sûr, diminue et diminue. Le reste, je pense, est compréhensible. Il est à noter que la réputation acquise donne aux organisateurs le temps de se cacher avec succès d'Ivan Vasilyevich, qui s'est retrouvé non seulement sans lot de boulons, mais également sans pantalon.

Nous reviendrons un peu plus loin sur des exemples non moins curieux, mais pour l'instant, le suivant est peut-être le cas le plus courant avec trois hypothèses :

Problème 7

Les lampes électriques sont fabriquées dans trois usines. La 1ère usine produit 30% du nombre total de lampes, la 2ème - 55% et la 3ème - le reste. Les produits de la 1ère usine contiennent 1% de lampes défectueuses, la 2ème - 1,5%, la 3ème - 2%. Le magasin reçoit des produits des trois usines. La lampe achetée s'est avérée défectueuse. Quelle est la probabilité qu'il ait été produit par la 2ème usine ?

Notez que dans les problèmes sur les formules de Bayes dans la condition nécessairement il y a une certaine Qu'est-il arrivéévénement, en l'occurrence l'achat d'une lampe.

Le nombre d'événements a augmenté et Solution il est plus pratique d'arranger dans un style "rapide".

L'algorithme est exactement le même: à la première étape, nous trouvons la probabilité que la lampe achetée du tout s'avérera défectueux.

À partir des données initiales, nous traduisons les pourcentages en probabilités :
- les probabilités que la lampe soit produite respectivement par les 1ère, 2ème et 3ème usines.
Contrôler:

De même : - la probabilité de fabriquer une lampe défectueuse pour les usines respectives.

D'après la formule de probabilité totale :

- la probabilité que la lampe achetée soit défectueuse.

Deuxième étape. Supposons que la lampe achetée s'avère défectueuse (l'événement s'est produit)

D'après la formule de Bayes :
- la probabilité que la lampe défectueuse achetée ait été fabriquée par une deuxième usine

Réponse:

Pourquoi la probabilité initiale de la 2e hypothèse a-t-elle augmenté après la réévaluation ? Après tout, la deuxième usine produit des lampes de qualité moyenne (la première est meilleure, la troisième est pire). Alors pourquoi a-t-il augmenté a postériori la probabilité que la lampe défectueuse provienne de la 2ème usine ? Ce n'est plus dû à la "réputation", mais à la taille. Puisque l'usine numéro 2 a produit le plus grand nombre de lampes, il est (au moins subjectivement) blâmé : "Très probablement, cette lampe défectueuse vient de là".

Il est intéressant de noter que les probabilités des 1ère et 3ème hypothèses ont été surestimées dans les directions attendues et sont devenues égales :

Contrôler: , ce qui devait être vérifié.

À propos des estimations sous-estimées et surestimées :

Problème 8

Dans le groupe étudiant, 3 personnes ont un niveau de formation élevé, 19 personnes ont un niveau moyen et 3 ont un niveau faible. Les probabilités de réussite à l'examen pour ces étudiants sont respectivement égales : 0,95 ; 0,7 et 0,4. On sait qu'un certain élève a réussi l'examen. Quelle est la probabilité que :

a) il était très bien préparé ;
b) a été préparé moyen ;
c) était mal préparé.

Effectuer des calculs et analyser les résultats de la réévaluation des hypothèses.

La tâche est proche de la réalité et est particulièrement plausible pour un groupe d'étudiants par correspondance, où l'enseignant ne connaît pratiquement pas les capacités de tel ou tel élève. Dans ce cas, le résultat peut entraîner des conséquences assez inattendues. (surtout pour les examens du 1er semestre)... Si un élève mal préparé a la chance d'avoir un billet, alors l'enseignant est susceptible de le considérer comme un bon élève ou même un élève fort, ce qui apportera de bons dividendes à l'avenir. (naturellement, il faut "mettre la barre plus haut" et entretenir son image)... Si un étudiant a enseigné, s'est entassé, a répété pendant 7 jours et 7 nuits, mais qu'il n'a tout simplement pas eu de chance, alors d'autres événements peuvent se développer de la pire des manières - avec de nombreuses reprises et un équilibre sur le point de partir.

Inutile de dire que la réputation est le capital le plus important, ce n'est pas un hasard si de nombreuses sociétés portent les noms et prénoms de leurs pères fondateurs, qui ont dirigé l'entreprise il y a 100-200 ans et sont devenus célèbres pour leur réputation irréprochable.

Oui, l'approche bayésienne est subjective dans une certaine mesure, mais... c'est ainsi que fonctionne la vie !

Consolidons le matériel avec un dernier exemple industriel, dans lequel je parlerai des subtilités techniques de la solution qui n'ont pas encore été rencontrées :

Problème 9

Trois ateliers de l'usine produisent le même type de pièces, qui sont envoyées pour assemblage dans un conteneur commun. On sait que le premier atelier produit 2 fois plus de pièces que le deuxième atelier, et 4 fois plus que le troisième atelier. Dans le premier magasin, la ferraille est de 12%, dans le second - 8%, dans le troisième - 4%. Pour le contrôle, une partie est prélevée dans le conteneur. Quelle est la probabilité qu'elle soit défectueuse ? Quelle est la probabilité que la pièce défectueuse récupérée ait été libérée par le 3ème atelier ?

Taki Ivan Vasilyevich est de retour à cheval =) Le film doit avoir une fin heureuse =)

Solution: contrairement aux problèmes n° 5-8, ici la question est explicitement posée, qui est résolue en utilisant la formule de probabilité totale. Mais d'un autre côté, la condition est un peu "cryptée", et l'habileté de l'école à composer les équations les plus simples nous aidera à résoudre cette énigme. Il est pratique de prendre la plus petite valeur pour "x":

Soit la proportion de pièces produites par le troisième atelier.

Par condition, la première boutique produit 4 fois plus que la troisième boutique, donc la part de la 1ère boutique est.

De plus, le premier atelier produit 2 fois plus de produits que le deuxième atelier, ce qui signifie que la part de ce dernier est de :.

Composons et résolvons l'équation :

Ainsi : - les probabilités que la pièce sortie du conteneur ait été libérée par les 1er, 2e et 3e magasins respectivement.

Contrôler: . De plus, il ne sera pas superflu de revoir la phrase "On sait que la première boutique fabrique 2 fois plus de produits que la deuxième boutique et 4 fois plus que la troisième boutique." et assurez-vous que les valeurs de probabilités obtenues correspondent bien à cette condition.

Initialement, la part du 1er ou la part du 2ème atelier pourrait être prise pour "X" - les probabilités seront les mêmes. Mais, d'une manière ou d'une autre, la section la plus difficile a été franchie, et la solution entre dans l'ornière moletée :

A partir de la condition on trouve :
- la probabilité de fabrication de pièces défectueuses pour les ateliers respectifs.

D'après la formule de probabilité totale :
- la probabilité qu'une pièce prise au hasard dans le conteneur soit non standard.

Question 2 : quelle est la probabilité que la pièce défectueuse récupérée soit restituée par le 3ème atelier ? Cette question suppose que la pièce a déjà été récupérée et s'avère défectueuse. Nous réévaluons l'hypothèse bayésienne :
est la probabilité requise. Tout à fait attendu - après tout, le troisième atelier produit non seulement la plus petite fraction de pièces, mais aussi un leader en termes de qualité !

Dans ce cas, j'ai dû simplifier une fraction de quatre étages, ce qui dans les problèmes sur les formules de Bayes doit être fait assez souvent. Mais pour cette leçon, j'ai accidentellement choisi des exemples dans lesquels de nombreux calculs peuvent être effectués sans fractions ordinaires.

Étant donné que la condition ne contient pas les éléments "a" et "b", il est préférable de fournir la réponse avec des commentaires textuels :

Réponse: - la probabilité que la pièce retirée du conteneur soit défectueuse ; - la probabilité que la pièce défectueuse récupérée ait été libérée par le 3ème atelier.

Comme vous pouvez le voir, les problèmes de la formule de probabilité totale et des formules de Bayes sont assez simples et, probablement, pour cette raison, ils essaient souvent de compliquer la condition qu'elles contiennent, que j'ai déjà mentionnée au début de l'article.

Plus d'exemples sont dans le fichier avec des solutions prêtes à l'emploi pour F.P.V. et formules de Bayes, d'ailleurs, il y aura probablement ceux qui voudront se familiariser plus profondément avec ce sujet dans d'autres sources. Et le sujet est vraiment très intéressant - qui n'en vaut qu'un Paradoxe de Bayes, qui corrobore ce conseil quotidien selon lequel si une personne est diagnostiquée avec une maladie rare, il est alors logique qu'elle procède à un deuxième ou même deux examens indépendants répétés. Il semblerait que cela se fasse uniquement par désespoir... - mais non ! Mais ne parlons pas de choses tristes.

- la probabilité qu'un étudiant choisi au hasard réussisse l'examen.
Faire réussir l'examen à l'élève. D'après les formules de Bayes :
une) - la probabilité que l'étudiant qui a réussi l'examen ait été très bien préparé. La probabilité initiale objective s'avère être surestimée, puisque presque toujours certains « paysans moyens » ont de la chance avec les questions et ils répondent très fortement, ce qui donne l'impression erronée d'une préparation impeccable.
b) - la probabilité que l'étudiant ayant réussi l'examen ait une préparation moyenne. La probabilité initiale s'avère légèrement surestimée, puisque les étudiants avec un niveau de formation moyen sont généralement majoritaires, de plus, ici l'enseignant inclura des "excellents étudiants" sans succès, et parfois un élève peu performant qui a eu beaucoup de chance avec un ticket.
v) - la probabilité que l'étudiant ayant réussi l'examen ait été mal préparé. La probabilité initiale a été surestimée pour le pire. Pas étonnant.
Examen:
Réponse :

Commençons par un exemple. Dans l'urne devant toi avec une probabilité égale il peut y avoir (1) deux boules blanches, (2) une blanche et une noire, (3) deux noires. Vous faites glisser la balle et elle s'avère être blanche. Comment évaluez-vous maintenant probabilité ces trois options (hypothèses) ? Évidemment, la probabilité de l'hypothèse (3) avec deux boules noires = 0. Mais comment calculer les probabilités des deux hypothèses restantes !? Cela permet de faire la formule de Bayes, qui dans notre cas a la forme (le numéro de la formule correspond au numéro de l'hypothèse testée) :

Téléchargez une note au format ou

X- une variable aléatoire (hypothèse) prenant des valeurs : x 1- deux blancs, x 2- un blanc, un noir ; x 3- deux noirs ; à- une variable aléatoire (événement) prenant des valeurs : à 1- la boule blanche est retirée et à 2 heures- a sorti une boule noire ; P (x 1) Est la probabilité de la première hypothèse avant de retirer la balle ( a priori probabilité ou vraisemblance avant de expérience) = 1/3 ; P (x 2)- probabilité de la deuxième hypothèse avant de sortir la balle = 1/3 ; P (x 3)- probabilité de la troisième hypothèse avant de sortir la balle = 1/3 ; P (y 1|x 1)- la probabilité conditionnelle de sortir une boule blanche, si la première hypothèse est vraie (boules blanches) = 1 ; P (y 1|x 2) – la probabilité de retirer une boule blanche si la deuxième hypothèse est vraie (une boule est blanche, l'autre est noire) = ½ ; P (y 1|x 3) – la probabilité de retirer la boule blanche, si la troisième hypothèse est vraie (les deux noirs) = 0 ; P (y 1)- la probabilité de retirer la boule blanche = ½ ; P (y 2)- la probabilité de sortir la boule noire = ½ ; et enfin ce que nous recherchons - P (x 1|à 1) – la probabilité que la première hypothèse soit vraie (les deux boules blanches), à condition de sortir une boule blanche ( a postériori probabilité ou vraisemblance après de l'expérience); P (x 2|à 1) – la probabilité que la deuxième hypothèse soit vraie (une boule est blanche, l'autre est noire), à ​​condition d'avoir tiré une boule blanche.

La probabilité que la première hypothèse soit vraie (deux blanches), à condition de sortir une boule blanche :

La probabilité que la deuxième hypothèse soit vraie (l'une est blanche, l'autre est noire), à ​​condition de sortir une boule blanche :

La probabilité que la troisième hypothèse soit vraie (deux noires), à condition de sortir une boule blanche :

A quoi sert la formule de Bayes ? Il permet, sur la base des probabilités a priori des hypothèses - P (x 1), P (x 2), P (x 3)- et les probabilités d'occurrence des événements - P (y 1), P (y 2)- calculer les probabilités postérieures des hypothèses, par exemple, la probabilité de la première hypothèse, à condition qu'une boule blanche soit tirée - P (x 1|à 1).

Revenons à la formule (1). La probabilité initiale de la première hypothèse était P (x 1) = 1/3. Avec probabilité P (y 1) = 1/2 nous pourrions retirer la boule blanche, et avec la probabilité P (y 2) = 1/2- noir. Nous avons sorti le blanc. Probabilité d'arracher le blanc, à condition que la première hypothèse soit vraie P (y 1|x 1) = 1. La formule de Bayes dit que depuis que nous avons retiré le blanc, la probabilité de la première hypothèse a augmenté à 2/3, la probabilité de la deuxième hypothèse est toujours de 1/3 et la probabilité de la troisième hypothèse a disparu.

Il est facile de vérifier que si l'on retirait la boule noire, les probabilités postérieures changeraient symétriquement : P (x 1|y 2) = 0, P (x 2|y 2) = 1/3, P (x 3|y2) = 2/3.

Voici ce que Pierre Simon Laplace a écrit à propos de la formule de Bayes dans un ouvrage publié en 1814 :

C'est le principe de base de la branche de l'analyse du hasard qui traite de la transition des événements aux causes.

Pourquoi la formule de Bayes est-elle si difficile à comprendre !? À mon avis, parce que notre approche habituelle est de raisonner de cause à effet. Par exemple, s'il y a 36 boules dans l'urne, dont 6 sont noires et les autres sont blanches. Quelle est la probabilité de retirer la boule blanche ? La formule de Bayes permet de passer des événements aux causes (hypothèses). Si nous avions trois hypothèses et qu'un événement se produisait, comment exactement cet événement (et non un autre) a-t-il affecté les probabilités initiales des hypothèses ? Comment ces probabilités ont-elles changé ?

Je crois que la formule de Bayes ne concerne pas seulement les probabilités. Il change le paradigme de la perception. Quel est le train de la pensée lors de l'utilisation du paradigme déterministe? Si un événement se produit, quelle en est la cause ? S'il y a un accident, une urgence, un conflit militaire. A qui ou quoi était leur faute ? Qu'en pense un observateur bayésien ? Quelle est la structure de la réalité qui a conduit à donné cas de telle ou telle manifestation... le bayésien comprend qu'en autrement le résultat aurait pu être différent...

Plaçons les symboles dans les formules (1) et (2) un peu différemment :

Parlons encore de ce que nous voyons. L'une des trois hypothèses pourrait être vraie avec une probabilité initiale (antérieure) égale. Nous aurions pu tirer une boule blanche ou noire avec une probabilité égale. Nous avons sorti le blanc. Au vu de ces nouvelles informations complémentaires, notre appréciation des hypothèses devrait être revue. La formule de Bayes vous permet de le faire numériquement. La probabilité a priori de la première hypothèse (formule 7) était P (x 1), a sorti une boule blanche, la probabilité postérieure de la première hypothèse est devenue P (x 1|à 1). Ces probabilités diffèrent par un facteur.

Événement à 1 est appelé preuve, confirmant ou réfutant plus ou moins l'hypothèse x 1... Ce ratio est parfois appelé le pouvoir du certificat. Plus la preuve est puissante (plus le coefficient diffère de un), plus le fait d'observation est important à 1 change la probabilité a priori, plus la probabilité a posteriori diffère de la probabilité a priori. Si la preuve est faible (coefficient ~ 1), la probabilité postérieure est presque égale à la probabilité antérieure.

Certificat à 1 v = 2 fois changé la probabilité a priori de l'hypothèse x 1(formule 4). Parallèlement, le témoignage à 1 n'a pas changé la probabilité de l'hypothèse x 2 depuis sa puissance = 1 (formule 5).

En général, la formule de Bayes ressemble à ceci :

X- une variable aléatoire (un ensemble d'hypothèses mutuellement exclusives), prenant des valeurs : x 1, x 2, … , Xm. à- une variable aléatoire (un ensemble d'événements mutuellement exclusifs), prenant des valeurs : à 1, à 2 heures, … , àm. La formule de Bayes permet de trouver la probabilité postérieure de l'hypothèse Xje lorsqu'un événement se produit oui j... Le numérateur est le produit de la probabilité a priori de l'hypothèse Xje – P (xje) sur la probabilité d'un événement oui j si l'hypothèse est vraie Xje – R(oui j| xje). Le dénominateur est la somme des produits du même qu'au numérateur, mais pour toutes les hypothèses. Si nous calculons le dénominateur, nous obtenons la probabilité totale d'occurrence de l'événement àj(si l'une des hypothèses est vraie) - R(oui j) (comme dans les formules 1-3).

Encore une fois sur le témoignage. Événement oui j fournit des informations supplémentaires qui nous permettent de réviser la probabilité a priori de l'hypothèse Xje... Le pouvoir du certificat est - contient au numérateur la probabilité de l'événement oui j si l'hypothèse est vraie Xje... Le dénominateur est la probabilité totale que l'événement se produise àj(ou la probabilité qu'un événement se produise àj moyenne sur toutes les hypothèses). àj ci-dessus pour l'hypothèse Xje que la moyenne pour toutes les hypothèses, alors la preuve fait le jeu de l'hypothèse Xje augmenter sa probabilité postérieure R(oui j| xje). Si la probabilité qu'un événement se produise àj ci-dessous pour l'hypothèse Xje que la moyenne pour toutes les hypothèses, alors la preuve abaisse la probabilité postérieure R(oui j| xje) pour hypothèses Xje. Si la probabilité qu'un événement se produise àj pour hypothèse Xje est la même que la moyenne pour toutes les hypothèses, alors la preuve ne change pas la probabilité postérieure R(oui j| xje) pour hypothèses Xje.

Voici quelques exemples qui, j'espère, renforceront votre compréhension de la formule de Bayes.

Problème 2. Deux tireurs indépendamment l'un de l'autre tirent sur la même cible, chacun faisant un tir. La probabilité de toucher la cible pour le premier tireur est de 0,8, pour le second de 0,4. Après le tir, un trou a été trouvé dans la cible. Trouvez la probabilité que ce trou appartienne au premier tireur. ...

Tâche 3. L'objet surveillé peut être dans l'un des deux états suivants : H 1 = (fonctionne) et H 2 = (ne fonctionne pas). Les probabilités a priori de ces états sont P (H 1) = 0,7, P (H 2) = 0,3. Il existe deux sources d'informations qui fournissent des informations contradictoires sur l'état de l'objet ; la première source rapporte que l'objet ne fonctionne pas, la seconde - qu'il fonctionne. On sait que la première source donne des informations correctes avec une probabilité de 0,9 et avec une probabilité de 0,1 - erronée. La deuxième source est moins fiable : elle donne des informations correctes avec une probabilité de 0,7, et avec une probabilité de 0,3 - erronées. Trouver les probabilités postérieures des hypothèses. ...

Les problèmes 1 à 3 sont tirés du manuel de ES Ventzel, LA Ovcharov. La théorie des probabilités et ses applications en ingénierie, section 2.6 Théorème d'hypothèse (formule de Bayes).

Le problème 4 est tiré du livre, section 4.3 Théorème de Bayes.

Lors du calcul de la formule de la probabilité totale, il a été supposé que l'événement UNE, dont la probabilité devait être déterminée, pourrait se produire avec l'un des événements N 1 , H 2 , ... , Hn formant un groupe complet d'événements incompatibles par paires. De plus, les probabilités de ces événements (hypothèses) étaient connues à l'avance. Supposons qu'une expérience ait été réalisée, à la suite de laquelle l'événement UNE est venu. Cette information supplémentaire permet de réévaluer les probabilités des hypothèses. Salut, calculateur P (H i / A).

ou, en utilisant la formule de probabilité totale, nous obtenons

Cette formule est appelée formule de Bayes ou théorème d'hypothèse. La formule de Bayes vous permet de "réviser" les probabilités d'hypothèses après que le résultat de l'expérience, à la suite duquel l'événement est apparu, soit connu UNE.

Probabilités P (H je) Sont les probabilités a priori des hypothèses (elles sont calculées avant l'expérience). Les probabilités P (H i / A) Sont les probabilités postérieures des hypothèses (elles sont calculées après l'expérience). La formule de Bayes permet de calculer les probabilités postérieures par leurs probabilités antérieures et par les probabilités conditionnelles de l'événement UNE.

Exemple... On sait que 5% de tous les hommes et 0,25% de toutes les femmes sont daltoniens. La personne choisie au hasard par le numéro de la carte médicale souffre de daltonisme. Quelle est la probabilité qu'il s'agisse d'un homme ?

Solution... Événement UNE- une personne souffre de daltonisme. L'espace des événements élémentaires pour l'expérience - une personne est sélectionnée par le numéro d'une carte médicale - Ω = ( N 1 , H 2 ) se compose de 2 événements :

N 1 - un homme est sélectionné,

N 2 - une femme est sélectionnée.

Ces événements peuvent être choisis comme hypothèses.

Par la condition du problème (choix aléatoire), les probabilités de ces événements sont les mêmes et égales P (H 1 ) = 0.5; P (H 2 ) = 0.5.

Dans ce cas, les probabilités conditionnelles qu'une personne souffre de daltonisme sont respectivement égales :

P (A / H 1 ) = 0.05 = 1/20; P (A / H 2 ) = 0.0025 = 1/400.

Comme on sait que la personne choisie est daltonienne, c'est-à-dire que l'événement s'est produit, on utilise la formule de Bayes pour réévaluer la première hypothèse :

Exemple. Il y a trois boîtes du même type. Dans la première case, il y a 20 boules blanches, dans la seconde - 10 blanches et 10 noires, dans la troisième - 20 boules noires. Une boule blanche a été sortie d'une boîte choisie au hasard. Calculez la probabilité que la balle soit retirée de la première case.

Solution... Notons par UNEévénement - l'apparition d'une boule blanche. Trois hypothèses (hypothèses) peuvent être faites sur le choix de la boîte : N 1 ,N 2 , N 3 - sélection des première, deuxième et troisième cases, respectivement.

Le choix de n'importe laquelle des cases étant également possible, les probabilités des hypothèses sont les mêmes :

P (H 1 ) = P (H 2 ) = P (H 3 )= 1/3.

Par la condition du problème, la probabilité d'extraire une boule blanche de la première case est

Probabilité de retirer la boule blanche de la deuxième case

Probabilité de retirer la boule blanche de la troisième case

La probabilité requise est trouvée par la formule de Bayes :

Répétition des tests. La formule de Bernoulli.

N tests sont effectués, dans chacun desquels l'événement A peut ou non se produire, et la probabilité de l'événement A dans chaque test individuel est constante, c'est-à-dire ne change pas d'une expérience à l'autre. Nous savons déjà comment trouver la probabilité de l'événement A dans une expérience.

La probabilité d'occurrence d'un certain nombre de fois (m fois) de l'événement A dans n expériences est particulièrement intéressante. de tels problèmes sont facilement résolus si les tests sont indépendants.

Déf. Plusieurs tests sont appelés indépendant par rapport à l'événement A si la probabilité de l'événement A dans chacun d'eux ne dépend pas des résultats d'autres expériences.

La probabilité n (m) d'occurrence de l'événement A exactement m fois (non-occurrence n-m fois, événement) dans ces n tests. L'événement A apparaît dans des séquences m fois très différentes).

- La formule de Bernoulli.

Les formules suivantes sont évidentes :

n (m moins k fois dans n tests.

P n (m> k) = P n (k + 1) + P n (k + 2) +… + P n (n) est la probabilité d'occurrence de l'événement A Suite k fois dans n tests.