1 signe d'égalité des triangles est appelé. Le premier signe d'égalité des triangles

Billet 2

question 1

Tests d'égalité des triangles (preuve de tout)

1er signeégalité des triangles : sur deux côtés et l'angle entre eux ( Théorème 3.1. – Signe d'égalité des triangles par deux côtés et l'angle entre eux - Si deux côtés et l'angle entre eux d'un triangle sont égaux, respectivement, à deux côtés et l'angle entre eux d'un autre triangle, alors ces triangles sont congrus)

Preuve:

Soit les triangles ABC et A 1 B 1 C 1 ont un angle A égal à l'angle A 1, AB égal à A 1 B 1, AC égal à A 1 C 1, prouvons que les triangles sont égaux.

Puisque A 1 B 1 est égal à A 1 B 2, alors le sommet B 2 coïncidera avec B 1. Puisque l'angle B 1 A 1 C 1 est égal à l'angle B 2 A 1 C 2, alors le rayon A 1 C 2 coïncidera avec A 1 C 1 . Puisque A 1 C 1 est égal à A 1 C 2, alors C 2 coïncidera avec C 1. Cela signifie que le triangle A 1 B 1 C 1 coïncide avec le triangle A 1 B 2 C 2, ce qui signifie qu'il est égal à le triangle ABC.

Le théorème a été prouvé.

2ème signeégalité des triangles : le long des angles latéraux et adjacents (Théorème 3.2. - Signe d'égalité des triangles par côté et angles adjacents - Si un côté et ses angles adjacents d'un triangle sont égaux, respectivement, au côté et aux angles adjacents d'un autre triangle, alors ces triangles sont congrus)

Preuve:

Laisser ABC et A 1 B 1 C 1 sont deux triangles dans lesquels AB est égal à A 1 B 1, l'angle A est égal à l'angle A 1 et l'angle B est égal à l'angle B 1. Montrons qu'ils sont égaux.

Soit A 1 B 2 C 2 un triangle égal à ABC, de sommet B 2 sur le rayon A 1 B 1 et de sommet C 2 dans le même demi-plan par rapport à la droite A 1 B 1, où se trouve le sommet C 1.

Puisque A 1 B 2 est égal à A 1 B 1, alors le sommet B 2 coïncidera avec B 1. Puisque l'angle B 1 A 1 C 2 est égal à l'angle B 1 A 1 C 1 et que l'angle A1B1C2 est égal à l'angle A1B1C1, alors le rayon A 1 C 2 coïncidera avec A 1 C 1, et B 1 C 2 coïncidera avec B 1 C 1. Il s'ensuit que le sommet C 2 coïncide avec C 1. Cela signifie que le triangle A 1 B 1 C 1 coïncide avec le triangle A 1 B 2 C 2, ce qui signifie qu'il est égal au triangle ABC.

Le théorème a été prouvé.

3ème signeégalité des triangles : sur trois côtés (Théorème 3.6. - Test d'égalité des triangles sur trois côtés - Si trois côtés d'un triangle sont égaux, respectivement, à trois côtés d'un autre triangle, alors ces triangles sont congrus)

Preuve:

Laisser ABC et A 1 B 1 C 1 sont deux triangles dans lesquels AB est égal à A 1 B 1, AC est égal à A 1 C 1 et BC est égal à B 1 C 1. Montrons qu'ils sont égaux.

Disons que les triangles ne sont pas égaux. Alors leur angle A n'est pas égal à l'angle A 1, l'angle B n'est pas égal à l'angle B 1 et l'angle C n'est pas égal à l'angle C 1. Sinon, ils seraient égaux, sur la base des plumes.

Soit A 1 B 1 C 2 un triangle égal au triangle ABC, dont le sommet C 2 se trouve dans le même demi-plan que le sommet C 1 par rapport à la droite A 1 B 1.

Soit D le milieu du segment C 1 C 2. Les triangles A 1 C 1 C 2 et B 1 C 1 C 2 sont isocèles de base commune C 1 C 2. Par conséquent, leurs médianes A 1 D et B 1 D sont des hauteurs, ce qui signifie que les lignes A 1 D et B 1 D sont perpendiculaires à la ligne C 1 C 2. Les lignes A 1 D et B 1 D ne coïncident pas, puisque les points A 1, B 1 , D ne se trouvent pas sur la même ligne, mais passant par le point D de la ligne C 1 C 2, une seule ligne perpendiculaire à celui-ci peut être tracée. Nous sommes arrivés à une contradiction.

Dans cet article, nous vous expliquerons comment formuler et prouver premier signe d'égalité des triangles qui se déroule en 7e année.

Formulation du premier signe d'égalité des triangles

"Si deux côtés et l'angle qu'ils forment d'un triangle sont égaux à deux côtés et l'angle qu'ils forment d'un autre triangle, alors ces triangles sont congrus."

C'est ce qu'on appelle l'égalité en abrégé "de deux côtés et l'angle qui les sépare."

Avant de poursuivre, il faut rappeler ce qu’on appelle un triangle et dans quel cas on peut dire que deux triangles sont égaux.

Qu'est-ce qu'un triangle et quand sont-ils considérés comme égaux ?

Triangle est une figure géométrique de trois segments reliant trois points (à condition qu'ils ne se trouvent pas sur la même ligne droite. Ces points sont considérés pics Triangle. Et les segments qui les relient sont des soirées).

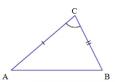
La figure 1 montre le triangle ABC. Qui a trois sommets (A, B et C). Et les côtés sont AB, AC et BC.

Image 1

Les triangles sont considérés comme égaux lorsque tous leurs côtés et angles sont respectivement égaux entre eux (dans le cas où seuls les angles sont égaux et les côtés sont proportionnels, les triangles sont appelés similaire). Ainsi, il est évident que des triangles égaux peuvent se superposer - et ils coïncideront complètement.

Preuve du premier signe d'égalité des triangles

Donné:

Deux triangles : ABC et DEF (Figure 2).

Figure 2

D'après les conditions du théorème, deux paires de segments de ces triangles sont égales entre elles (AC = FD et CB = EF). Les angles entre les segments sont également égaux (c'est-à-dire ∠ACV = ∠EFD).

Prouver ce triangle ABC est égal au triangle DEF.

Preuve:

1. Puisqu'il y a égalité des angles (∠ACB = ∠EFD), les triangles peuvent se superposer les uns aux autres pour que le sommet C coïncide avec le sommet F.
2. Dans ce cas, les segments CA et CB chevaucheront les segments FE et FD.
3. Et puisque les segments de deux triangles sont égaux entre eux (AC = FD et CB = EF par condition), alors le segment AB coïncidera également avec le côté ED.
4. Cela entraînera à son tour la combinaison des sommets A et D, B et E.
5. Par conséquent, les triangles s’emboîtent complètement, ce qui signifie qu’ils sont égaux.

Le théorème a été prouvé.

Dans cette leçon, nous étudierons le premier signe d'égalité des triangles. Tout d’abord, nous formulons et prouvons le théorème sur le premier critère d’égalité des triangles. Ensuite, nous résoudrons des problèmes en utilisant le premier signe d’égalité des triangles.

Dans la leçon précédente, nous avons introduit le concept de « triangles égaux » - des triangles qui peuvent être combinés par chevauchement. Cependant, il est très difficile de comparer des chiffres par définition, nous allons donc introduire des critères d'égalité des triangles - selon certains éléments.

Riz. 1. Les triangles ABC et A 1 B 1 C 1 sont égaux

Démontrons le théorème : si deux côtés et l'angle entre eux d'un triangle et les deux côtés correspondants et l'angle entre eux du deuxième triangle sont égaux, alors ces triangles sont congrus.

Théorème : Donné. Prouver : ABC et .

Preuve : superposons les données dans la condition des formes. À la suite de cette action, les sommets A et A 1, les segments AB et A 1 B 1, AC et A 1 C 1 coïncident. Si l’on considère les triangles dans leur ensemble, cela coïncidera avec .

Le théorème a été prouvé.

Considérons plusieurs problèmes.

Les segments AC et BD sont divisés en deux par leur point d'intersection O. Prouve-le .

Preuve : Faisons un dessin explicatif.

Riz. 2. Dessiner par exemple 1

Notez que les angles AOB et COD sont égaux, comme les angles verticaux, et que les côtés BO et AO du triangle AOB sont respectivement égaux aux côtés OD et OC du triangle COD. Les triangles AOB et COD sont donc égaux selon le premier critère.

Les segments AC et BD sont divisés en deux par le point d'intersection. Prouve-le .

Riz. 3. Dessiner par exemple 2

Dans le problème précédent, nous avons prouvé cela d’après le premier signe. De ces considérations nous pouvons conclure que AB = CD, ∠OAB = ∠OCD.

Maintenant regardons les triangles . Ils ont AC - un côté commun, AB = CD et ∠CAB = ∠ACD (comme prouvé). Donc selon le premier signe d’égalité. Q.E.D.

Riz. 4. Dessiner par exemple 3

Sur la figure 3, les segments AB et AC sont égaux. L'angle 1 est égal à l'angle 2. On sait que AC = 15 cm, DC = 5 cm. Prouvez que . Trouvez les longueurs des segments BD et AB.

Les triangles sont égaux selon le premier critère, car ∠1 = ∠2, AB = AC et AD est le côté commun des deux triangles. De l'égalité des triangles il résulte que certains de leurs éléments correspondants sont égaux, donc : BD = CD = 5 cm,

AB = AC = 15 cm.

Réponse : 5 cm, 15 cm.

Dans la figure 5 BC = AD. L'angle 1 est égal à l'angle 2, AD = 17 cm, CD = 14 cm. Montrez que . Trouvez AB et BC.

Riz. 5. Dessin par exemple 4

Le triangle ABC est égal au triangle CDA. selon le premier signe. ∠1 = ∠2, CB = AD et AC est le côté commun des deux triangles. Il s'ensuit que .

1. Sujet de cours "Le premier signe d'égalité des triangles"
2. Triangle. Annuaire

1. N° 36. Butuzov V.F., Kadomtsev S.B., Prasolova V.V. Géométrie 7 / V.F. Butouzov, S.B. Kadomtsev, V.V. Prasolova, éd. Sadovnichego V.A. - M. : Éducation, 2010.

2. Montrer que les triangles BOA et EOC sont congrus. Les segments BE et AC sont divisés en deux par leur point d'intersection.

3. Montrer qu'une droite coupant des segments égaux des côtés d'un angle est perpendiculaire à sa bissectrice.

4. *Les segments égaux MA et MC sont tracés sur les côtés de l'angle M et on trace sa bissectrice sur laquelle est marqué le point B. Montrer que BM est la bissectrice de l'angle ABC.

1) de deux côtés et l'angle entre eux

Preuve:

Laissez les triangles ABC et A 1 B 1 C 1 avoir un angle A égal à l'angle A 1, AB égal à A 1 B 1, AC égal à A 1 C 1. Montrons que les triangles sont congrus.

Imposant le triangle ABC (ou symétrique à celui-ci) sur le triangle A 1 B 1 C 1 de sorte que l'angle A soit aligné avec l'angle A 1 . Puisque AB=A 1 B 1 et AC=A 1 C 1, alors B coïncidera avec B 1 et C coïncidera avec C 1. Cela signifie que le triangle A 1 B 1 C 1 coïncide avec le triangle ABC, et est donc égal au triangle ABC.

Le théorème a été prouvé.

2) le long des côtés et des coins adjacents

Preuve:

Soient ABC et A 1 B 1 C 1 deux triangles dans lesquels AB est égal à A 1 B 1, l'angle A est égal à l'angle A 1 et l'angle B est égal à l'angle B 1. Montrons qu'ils sont égaux.

Imposant le triangle ABC (ou symétrique à celui-ci) sur le triangle A 1 B 1 C 1 de sorte que AB coïncide avec A 1 B 1. Puisque ∠BAC =∠B 1 A 1 C 1 et ∠ABC=∠A 1 B 1 C 1, alors le rayon AC coïncidera avec A 1 C 1, et BC coïncideront avec B 1 C 1. Il s'ensuit que le sommet C coïncide avec C 1. Cela signifie que le triangle A 1 B 1 C 1 coïncide avec le triangle ABC, et est donc égal au triangle ABC.

Le théorème a été prouvé.

3) sur trois côtés

Preuve :

Considérons les triangles ABC et A l B l C 1, dans lesquels AB = A 1 B 1, BC = B l C 1 CA = C 1 A 1. Montrons que ΔАВС =ΔA 1 B 1 C 1.

Appliquons le triangle ABC (ou symétrique à celui-ci) au triangle A 1 B 1 C 1 de sorte que le sommet A soit aligné avec le sommet A 1 , le sommet B soit aligné avec le sommet B 1 et les sommets C et C 1 soient sur les côtés opposés de la ligne droite A 1 B 1 . Considérons 3 cas :

1) Le rayon C 1 C passe à l'intérieur de l'angle A 1 C 1 B 1. Puisque, selon les conditions du théorème, les côtés AC et A 1 C 1, BC et B 1 C 1 sont égaux, alors les triangles A 1 C 1 C et B 1 C 1 C sont isocèles. Par le théorème sur la propriété des angles d'un triangle isocèle, ∠1 = ∠2, ∠3 = ∠4, donc ∠ACB=∠A 1 C 1 B 1 .

2) Le rayon C 1 C coïncide avec l'un des côtés de cet angle. A repose sur CC 1. AC=A 1 C 1, BC=B 1 C 1, C 1 BC - isocèle, ∠ACB=∠A 1 C 1 B 1.

3) Le rayon C 1 C passe à l'extérieur de l'angle A 1 C 1 B 1. AC=A 1 C 1, BC=B 1 C 1, ce qui signifie ∠1 = ∠2, ∠1+∠3 = ∠2+∠4, ∠ACB=∠A 1 C 1 B 1.

Donc, AC=A 1 C 1, BC=B 1 C 1, ∠C=∠C 1. Par conséquent, les triangles ABC et A 1 B 1 C 1 sont égaux en
le premier critère d'égalité des triangles.

Le théorème a été prouvé.

2. Diviser un segment en n parties égales.

Tracez un rayon passant par A, disposez-y n segments égaux. Tracez une ligne droite passant par B et A n et des lignes parallèles passant par les points A 1 - A n -1. Marquons leurs points d'intersection avec AB. On obtient n segments égaux selon le théorème de Thales.

Théorème de Thalès. Si plusieurs segments égaux sont disposés successivement sur l'une des deux lignes et que des lignes parallèles sont tracées à travers leurs extrémités qui coupent la deuxième ligne, elles couperont alors des segments égaux sur la deuxième ligne.

Preuve. AB = CD

1. Tracez des lignes droites passant par les points A et C parallèles à l’autre côté de l’angle. On obtient deux parallélogrammes AB 2 B 1 A 1 et CD 2 D 1 C 1. D'après la propriété d'un parallélogramme : AB 2 = A 1 B 1 et CD 2 = C 1 D 1.

2. ΔABB 2 =ΔCDD 2 ABB 2 CDD 2 BAB 2 DCD 2 et sont égaux sur la base du deuxième critère d'égalité des triangles :
AB = CD selon le théorème,
comme correspondants, formés à l'intersection des droites parallèles BB 1 et DD 1 BD.

3. De même, chacun des angles s'avère égal à l'angle avec le sommet au point d'intersection des sécantes. AB 2 = CD 2 comme éléments correspondants dans des triangles congrus.

4. A 1 B 1 = AB 2 = CD 2 = C 1 D 1

Parmi le grand nombre de polygones, qui sont essentiellement une ligne brisée fermée et sans intersection, le triangle est la figure avec le moins d'angles. En d’autres termes, c’est le polygone le plus simple. Mais, malgré toute sa simplicité, cette figure regorge de nombreux mystères et découvertes intéressantes, qui sont éclairées par une branche particulière des mathématiques : la géométrie. Cette discipline commence à être enseignée dans les écoles à partir de la septième année, et le thème « Triangle » fait ici l'objet d'une attention particulière. Les enfants apprennent non seulement les règles concernant la figure elle-même, mais les comparent également en étudiant le 1er, le 2e et le 3e signe d'égalité des triangles.

Première rencontre

L'une des premières règles apprises par les écoliers ressemble à ceci : la somme des valeurs de tous les angles d'un triangle est égale à 180 degrés. Pour le confirmer, il suffit d'utiliser un rapporteur pour mesurer chacun des sommets et additionner toutes les valeurs résultantes. Sur cette base, avec deux quantités connues, il est facile de déterminer la troisième. Par exemple: Dans un triangle, l'un des angles fait 70° et l'autre fait 85°, quelle est la taille du troisième angle ?

180 - 85 - 70 = 25.

Réponse : 25°.

Les problèmes peuvent être encore plus complexes si une seule valeur d'angle est spécifiée et si la deuxième valeur est uniquement indiquée de combien ou de combien de fois elle est plus grande ou plus petite.

Dans un triangle, pour déterminer certaines de ses caractéristiques, des lignes spéciales peuvent être tracées, chacune ayant son propre nom :

• hauteur - une ligne droite perpendiculaire tracée du sommet vers le côté opposé ;
• les trois hauteurs, dessinées simultanément, se coupent au centre de la figure, formant un orthocentre qui, selon le type de triangle, peut être situé aussi bien à l'intérieur qu'à l'extérieur ;
• médiane - une ligne reliant le sommet au milieu du côté opposé ;
• l'intersection des médianes est le point de sa gravité, situé à l'intérieur de la figure ;
• bissectrice - une ligne allant d'un sommet au point d'intersection avec le côté opposé ; le point d'intersection de trois bissectrices est le centre du cercle inscrit.

Des vérités simples sur les triangles

Les triangles, comme toutes les formes, ont leurs propres caractéristiques et propriétés. Comme déjà mentionné, cette figure est le polygone le plus simple, mais avec ses propres caractéristiques :

• l'angle de plus grande valeur se situe toujours à l'opposé du côté le plus long, et vice versa ;
• Les angles égaux se trouvent face à des côtés égaux, un exemple en est un triangle isocèle ;
• la somme des angles internes est toujours égale à 180°, ce qui a déjà été démontré par exemple ;
• lorsqu'un côté d'un triangle s'étend au-delà de ses limites, il se forme un angle extérieur, qui sera toujours égal à la somme des angles qui ne lui sont pas adjacents ;
• chaque côté est toujours inférieur à la somme des deux autres côtés, mais supérieur à leur différence.

Types de triangles

La prochaine étape de connaissance consiste à déterminer le groupe auquel appartient le triangle présenté. L'appartenance à un type ou à un autre dépend de la taille des angles du triangle.

• Isocèle - avec deux côtés égaux, appelés latéraux, le troisième sert dans ce cas de base à la figure. Les angles à la base d'un tel triangle sont les mêmes, et la médiane tirée du sommet est la bissectrice et la hauteur.
• Un triangle régulier ou équilatéral est un triangle dont tous les côtés sont égaux.
• Rectangulaire : l'un de ses angles est de 90°. Dans ce cas, le côté opposé à cet angle s’appelle l’hypoténuse, et les deux autres s’appellent les jambes.
• Triangle aigu – tous les angles sont inférieurs à 90°.
• Obtus - l'un des angles supérieur à 90°.

Égalité et similitude des triangles

Au cours du processus d’apprentissage, ils considèrent non seulement une seule figure, mais comparent également deux triangles. Et ce sujet apparemment simple comporte de nombreuses règles et théorèmes permettant de prouver que les figures en question sont des triangles égaux. Les critères d'égalité des triangles ont la définition suivante : les triangles sont égaux si leurs côtés et angles correspondants sont les mêmes. Avec une telle égalité, si vous superposez ces deux figures, toutes leurs lignes convergeront. En outre, les chiffres peuvent être similaires, en particulier cela s'applique à des chiffres presque identiques qui ne diffèrent que par la taille. Afin de tirer une telle conclusion sur les triangles présentés, l'une des conditions suivantes doit être remplie :

• deux angles d'une figure sont égaux à deux angles d'une autre ;
• les deux côtés de l'un sont proportionnels aux deux côtés du second triangle, et les grandeurs des angles formés par les côtés sont égales ;
• trois côtés de la deuxième figure sont les mêmes que la première.

Bien entendu, pour une égalité incontestable qui ne soulèvera pas le moindre doute, il faut avoir les mêmes valeurs de tous les éléments des deux figures, cependant, avec l'utilisation de théorèmes, la tâche est grandement simplifiée, et seulement quelques-uns les conditions sont autorisées pour prouver l’égalité des triangles.

Le premier signe d'égalité des triangles

Les problèmes sur ce sujet sont résolus sur la base de la preuve du théorème, qui ressemble à ceci : « Si deux côtés d'un triangle et l'angle qu'ils forment sont égaux à deux côtés et à l'angle d'un autre triangle, alors les chiffres sont également égaux à l'un l'autre."

À quoi ressemble la preuve du théorème sur le premier signe d'égalité des triangles ? Tout le monde sait que deux segments sont égaux s’ils ont la même longueur, ou que les cercles sont égaux s’ils ont le même rayon. Et dans le cas des triangles, il existe plusieurs signes grâce auxquels nous pouvons supposer que les figures sont identiques, ce qui est très pratique à utiliser pour résoudre divers problèmes géométriques.

À quoi ressemble le théorème « Le premier signe d'égalité des triangles » est décrit ci-dessus, mais voici sa preuve :

• Supposons que les triangles ABC et A 1 B 1 C 1 aient les mêmes côtés AB et A 1 B 1 et, par conséquent, BC et B 1 C 1, et que les angles formés par ces côtés aient la même taille, c'est-à-dire qu'ils sont égaux. Ensuite, en superposant △ ABC sur △ A 1 B 1 C 1, on obtient la coïncidence de toutes les droites et sommets. Il s’ensuit que ces triangles sont absolument identiques, et donc égaux entre eux.

Le théorème « Le premier signe d'égalité des triangles » est aussi appelé « Sur deux côtés et un angle ». En fait, c'est son essence.

Théorème sur le deuxième signe

Le deuxième signe d'égalité est prouvé de la même manière ; la preuve est basée sur le fait que lorsque les figures se superposent, elles coïncident complètement sur tous les sommets et côtés. Et le théorème ressemble à ceci : « Si un côté et les deux angles à la formation desquels il participe correspondent au côté et aux deux angles du deuxième triangle, alors ces figures sont identiques, c'est-à-dire égales.

Troisième signe et preuve

Si les signes 2 et 1 d'égalité des triangles concernaient à la fois les côtés et les coins de la figure, alors le 3ème se réfère uniquement aux côtés. Ainsi, le théorème a la formulation suivante : « Si tous les côtés d'un triangle sont égaux aux trois côtés du deuxième triangle, alors les figures sont identiques. »

Pour prouver ce théorème, nous devons approfondir plus en détail la définition même de l’égalité. Au fond, que signifie l’expression « les triangles sont égaux » ? L'identité dit que si l'on superpose une figure sur une autre, tous leurs éléments coïncideront, cela ne peut être le cas que lorsque leurs côtés et leurs angles sont égaux. En même temps, l'angle opposé à l'un des côtés, qui est le même que celui de l'autre triangle, sera égal au sommet correspondant de la deuxième figure. Il convient de noter qu’à ce stade, la preuve peut facilement être traduite en 1 critère pour l’égalité des triangles. Si une telle séquence n’est pas respectée, l’égalité des triangles est tout simplement impossible, sauf dans les cas où la figure est l’image miroir de la première.

Triangles rectangles

La structure de tels triangles a toujours des sommets avec un angle de 90°. Par conséquent, les affirmations suivantes sont vraies :

• les triangles à angles droits sont égaux si les branches de l'un sont identiques à celles du second ;
• les figures sont égales si leurs hypoténuses et une de leurs jambes sont égales ;
• ces triangles sont congruents si leurs pattes et leur angle aigu sont identiques.

Ce signe fait référence à Pour prouver le théorème, ils appliquent l'application de figures les unes aux autres, à la suite de quoi les triangles sont pliés par les jambes de sorte que deux lignes droites avec les côtés CA et CA 1 sortent.

Utilisation pratique

Dans la plupart des cas, en pratique, le premier signe d'égalité des triangles est utilisé. En fait, un sujet de 7e année apparemment simple sur la géométrie et la planimétrie est également utilisé pour calculer la longueur, par exemple, d'un câble téléphonique sans mesurer la zone à travers laquelle il passera. Grâce à ce théorème, il est facile de faire les calculs nécessaires pour déterminer la longueur d'une île située au milieu de la rivière sans la traverser à la nage. Soit renforcez la clôture en plaçant la planche dans la travée de manière à la diviser en deux triangles égaux, soit calculez des éléments complexes du travail de menuiserie, ou lors du calcul du système de fermes de toit pendant la construction.

Le premier signe d’égalité des triangles est largement utilisé dans la vraie vie « adulte ». Bien que pendant les années scolaires, ce sujet particulier semble ennuyeux et totalement inutile pour beaucoup.