Champ d'une plaque infinie uniformément chargée. Application du théorème de Gauss pour calculer le champ d'un plan infini uniformément chargé

Nous supposerons que la charge est positive. Le plan est chargé avec une densité surfacique constante. De la symétrie, il s'ensuit que l'intensité en tout point du champ a une direction perpendiculaire au plan (Fig. 2.10). De toute évidence, aux points symétriques par rapport au plan, l'intensité du champ est la même en amplitude et en direction opposée.

Sélectionnez la zone sur le plan chargé. Entourons cette zone d'une surface fermée. En tant que surface fermée, nous représentons une surface cylindrique avec des génératrices perpendiculaires au plan et des bases de grandeur situées symétriquement par rapport au plan. On applique à cette surface le théorème de Gauss ... Il n'y aura pas d'écoulement à travers la partie latérale de la surface, puisqu'il est égal à zéro en chaque point. Pour les bases, c'est la même chose que. Par conséquent, le flux total à travers la surface sera égal. Il y a une charge à l'intérieur de la surface. D'après le théorème de Gauss, la condition suivante doit être satisfaite : 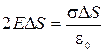, où . (3)

Le résultat obtenu ne dépend pas de la longueur du cylindre, c'est-à-dire à n'importe quelle distance du plan, l'intensité du champ est la même en amplitude. Le motif des lignes de tension ressemble à celui illustré à la Fig. 2.11. Pour un plan chargé négativement, les directions des vecteurs seront inversées. Si le plan est de dimensions finies, alors le résultat ne sera valable que pour les points dont la distance au bord de la plaque est très supérieure à la distance à la plaque elle-même (Fig. 2.12).

Trouvons la distribution du potentiel du champ créé par deux plaques parallèles identiques uniformément chargées, dont les charges sont égales en grandeur et opposées de signe 1 (fig. 279).

Riz. 279
Notons la densité de charge surfacique sur une plaque +σ et de l'autre −σ ... Distance entre les plaques h nous supposerons que les dimensions des plaques sont nettement plus petites. On introduit un système de coordonnées, l'axe z qui est perpendiculaire aux plaques, on place l'origine au milieu entre les plaques. Evidemment, pour des plaques infiniment grandes, toutes les caractéristiques du champ (intensité et potentiel) ne dépendent que de la coordonnée z... Pour calculer l'intensité du champ en divers points de l'espace, nous utilisons l'expression obtenue pour l'intensité du champ créé par une plaque infinie uniformément chargée et le principe de superposition.
Chaque plaque uniformément chargée crée un champ uniforme dont le module de résistance est égal à E o = / (2ε o), et les directions sont indiquées sur les figures 280, 281.



riz. 280

riz. 281
En additionnant les intensités de champ selon le principe de superposition, on trouve que dans l'espace entre les plaques, l'intensité de champ E = 2E o = / ε o deux fois l'intensité du champ d'une plaque (ici les champs des plaques individuelles sont parallèles), et il n'y a pas de champ en dehors des plaques (ici les champs des plaques individuelles sont opposés).
Au sens strict, pour les plaques de dimensions finies, le champ n'est pas uniforme ; les lignes de champ du champ de plaques de dimensions finies sont représentées sur la figure 282.



riz. 282
Les écarts les plus importants par rapport à l'uniformité sont observés près des bords des plaques (souvent ces écarts sont appelés effets de bord). Cependant, dans la zone adjacente au milieu des plaques, le champ avec haut degré la précision peut être considérée comme homogène, c'est-à-dire que les effets de bord peuvent être négligés dans ce domaine. A noter que plus le rapport de la distance entre les plaques sur leurs dimensions est petit, plus les erreurs de cette approximation sont faibles.
Pour déterminer sans ambiguïté la répartition du potentiel de champ, il est nécessaire de sélectionner le niveau du potentiel zéro. Nous supposerons que le potentiel est égal à zéro dans le plan situé au milieu entre les plaques, c'est-à-dire que nous mettons φ = 0 à z = 0.
Malgré l'arbitraire dans le choix du niveau zéro du potentiel, notre choix peut être logiquement justifié sur la base de la symétrie du système. En effet, le système de charges considéré se reflète en réflexion miroir par rapport au plan z = 0 et en même temps changer les signes des charges. Par conséquent, il est souhaitable que la distribution de potentiel ait la même symétrie : soit restaurée sous réflexion spéculaire avec un changement simultané du signe de toutes les fonctions de champ. La méthode choisie pour choisir le potentiel zéro satisfait à cette symétrie.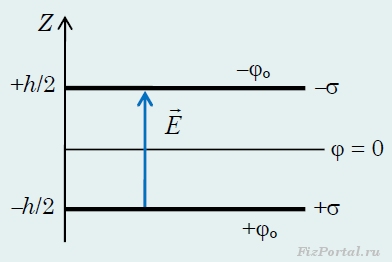



riz. 283
Notons le potentiel d'une plaque chargée positivement + φ o, alors le potentiel de la plaque chargée négativement sera égal à o... Ces potentiels sont faciles à déterminer en utilisant la valeur trouvée de l'intensité du champ entre les plaques et la relation entre la force et la différence de potentiel champ électrique... L'équation de cette connexion dans ce cas a la forme + φo - φ o = Eh... A partir de ce rapport, on détermine les valeurs des potentiels des plaques o = σh / (2ε o)... Compte tenu du fait que le champ est uniforme entre les plaques (donc, le potentiel change linéairement), et qu'il n'y a pas de champ en dehors des plaques (donc, le potentiel ici est constant), la dépendance du potentiel sur la coordonnée z a la forme (fig. 284)

riz. 284

 Tâches pour un travail indépendant.
 1. Dans tous les exemples considérés, faire l'opération inverse : en utilisant la distribution potentielle trouvée en utilisant la formule Ex = −Δφ / Δx calculer les forces des champs considérés.
 2. Déduire strictement la formule (6).
 3. Expliquez qualitativement le « paradoxe » suivant. Dans le domaine d'un condensateur plat, le potentiel de "l'infini" est défini de manière ambiguë : lors d'un déplacement dans le sens positif de l'axe Z le potentiel de "l'infini" s'est avéré être égal −φ o; lors d'un déplacement dans le sens négatif de l'axe Z − + φ o, en se déplaçant le long des axes X ou Oui- est égal à zéro. Quel est donc le potentiel de « l'infini » dans un système réel de deux plaques de dimensions finies ?

1 Un tel système est appelé condensateur plat ; nous étudierons ces dispositifs plus en détail plus tard.

Nous avons montré plus haut que champ électrique, créé par une plaque infinie uniformément chargée est homogène, c'est-à-dire que l'intensité du champ est la même en tous points, et le vecteur de force est dirigé perpendiculairement au plan et son module est E o = / (2ε o)... La famille les lignes électriques un tel champ est un ensemble de droites parallèles perpendiculaires à la plaque. En figue. 275, 276 montre également un graphique de la dépendance de la projection du vecteur d'intensité de champ Ez par axe Z perpendiculaire à la plaque (l'origine de cet axe sera située sur la plaque). Il est clair que le potentiel d'un champ donné ne dépend que de la coordonnée z, c'est-à-dire que les surfaces équipotentielles dans ce cas sont des plans parallèles à la plaque chargée.



riz. 275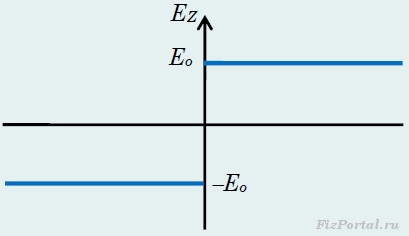



riz. 276
Avec le choix traditionnel du potentiel zéro (z → ∞), le potentiel d'un point arbitraire est égal au travail de déplacement d'une unité de charge positive d'un point donné à l'infini. Le module de tension étant constant, un tel travail (et, par conséquent, le potentiel) s'avère égal à l'infini ! Par conséquent, le choix spécifié du niveau de potentiel zéro ne convient pas dans ce cas.
Par conséquent, vous devez profiter de l'arbitraire du choix du niveau zéro. Il suffit de sélectionner un point arbitraire avec une coordonnée z = zo, et lui attribuer une valeur arbitraire du potentiel (z o) = o(fig. 277).

riz. 277
Maintenant, pour calculer la valeur du potentiel en un point arbitraire (z), vous pouvez utiliser la relation entre la force et le potentiel du champ

Tenant compte du fait que dans ce cas, l'intensité du champ est constante (à z> 0) cette expression s'écrit

d'où découle la dépendance recherchée du potentiel sur la coordonnée (à z> 0)

En particulier, on peut fixer une valeur arbitraire du potentiel de la plaque elle-même, c'est-à-dire mettre à z = z o = 0, = φ o... Ensuite, la valeur du potentiel en un point arbitraire est déterminée par la fonction

dont le graphique est illustré à la figure 278.

riz. 278
Le fait que le potentiel par rapport à l'infini se soit avéré infiniment grand est assez évident - après tout, une plaque infinie a également une charge infiniment grande. Comme nous l'avons déjà souligné, un tel système est une idéalisation - il n'y a pas de plaques infinies. En réalité, tous les corps ont des dimensions finies, donc pour eux le choix traditionnel du potentiel zéro est possible, bien que dans ce cas la répartition du champ puisse être très complexe. Dans le cadre de l'idéalisation envisagée, il est plus commode d'utiliser le choix du niveau zéro que nous avons utilisé.