Lettres en sopromat et leurs désignations. Fondamentaux de la résistance aux matériaux, formules de calcul
1. Concepts et hypothèses de base. Rigidité- la capacité d'une structure, dans certaines limites, à percevoir l'effet des forces extérieures sans destruction et sans modifications significatives des dimensions géométriques. Force- la capacité de la structure et de ses matériaux à résister aux charges. Durabilité- la capacité de la structure à conserver la forme de l'équilibre initial. Endurance- résistance des matériaux dans des conditions de charge. Hypothèse de continuité et d'uniformité : le matériau constitué d'atomes et de molécules est remplacé par un corps solide homogène. La continuité signifie qu'un volume arbitrairement petit contient une substance. L'homogénéité signifie qu'en tout point les propriétés du matériau sont les mêmes. L'utilisation de l'hypothèse vous permet d'appliquer le système. coordonnées et pour étudier les fonctions qui nous intéressent, utiliser l'analyse mathématique et décrire les actions avec différents modèles. Hypothèse d'isotropie : suppose que dans toutes les directions les îles saintes du matériau sont les mêmes. Arbre yavl anisotrope, dans lequel sv-va le long et à travers les fibres sont significativement différents.
2. Caractéristiques mécaniques du matériau. En dessous de seuil de rentabilité On entend par T la contrainte à laquelle la déformation croît sans augmentation notable de la charge. En dessous de limite élastique On entend par Y une telle contrainte maximale, jusqu'à laquelle le matériau ne reçoit pas de déformations résiduelles. Résistance à la traction(σ B) est le rapport de la force maximale que l'échantillon peut supporter à sa section transversale initiale. Limite proportionnelle(σ PR) - la contrainte la plus élevée, jusqu'à laquelle le matériau suit la loi de Hooke. La quantité E est le coefficient de proportionnalité, appelé module d'élasticité du premier type. Nom de la valeur G module de cisaillement ou module d'élasticité du 2ème type.(G = 0,5E / (1 + µ)). µ - le coefficient de proportionnalité sans dimension, appelé coefficient de Poisson, caractérise la propriété du matériau, est déterminé expérimentalement, pour tous les métaux, les valeurs numériques sont comprises entre 0,25 et 0,35.
3. Forces. L'interaction entre les parties de l'objet en question est har-yut Forces internes. Ils surviennent non seulement entre les unités individuelles en interaction de la structure, mais aussi entre toutes les particules adjacentes de l'objet sous charge. Les efforts internes sont déterminés par la méthode de la section. Distinguer superficiel et volumétrique forces externes. Les forces de surface peuvent être appliquées à de petites zones de la surface (ce sont des forces concentrées, telles que P) ou à des zones finies de la surface (ce sont des forces réparties, telles que q). Ils caractérisent l'interaction d'une structure avec d'autres structures ou avec l'environnement extérieur. Les forces volumétriques sont réparties sur le volume du corps. Ce sont les forces de gravité, les contraintes magnétiques, les forces d'inertie lors du mouvement accéléré de la structure.
4. Le concept de tension, tension admissible. Tension Est une mesure de l'intensité des forces internes Lim∆R / ∆F = p est la contrainte totale. La contrainte totale peut être décomposée en trois composantes : le long de la normale au plan de coupe et le long de deux axes dans le plan de coupe. La composante normale du vecteur de contrainte totale est notée et est appelée contrainte normale. Les composantes dans le plan de coupe sont appelées contraintes de cisaillement et notées τ. Tension admissible- [σ] = σ PREV / [n] - dépend de la qualité du matériau et du facteur de sécurité.
5. Déformation en traction-compression. S'étirer (serrer)- type de chargement, pour lequel des six facteurs de force internes (Qx, Qy, Mx, My, Mz, N), cinq sont égaux à zéro, et N 0. σ max = N max / F≤ [σ] + - condition de résistance à la traction ; σ max = N max / F≤ [σ] - - condition de résistance à la compression. L'expression mathématique de Zn Hooke : σ = εЕ, où ε = ∆L / L 0. ∆L = NL / EF - zone de Hooke élargie, où EF est la rigidité de la barre transversale. ε - déformation relative (longitudinale), ε '= ∆а / а 0 = ∆в / 0 - déformation transversale, où sous chargement а 0, 0 diminué de la valeur Δа = а 0 -а, ∆в = в 0 -v.
6. Caractéristiques géométriques des sections plates. Statique moment de l'aire : S x = ∫ydF, S y = ∫xdF, S x = y c F, S y = x c F. Pour une figure complexe S y = ∑S yi, S x = ∑S xi. Moments d'inertie axiaux: J x = y 2 dF, J y = ∫x 2 dF. Pour un rectangle J x = bh 3/12, J y = hb 3/12, pour un carré J x = J y = a 4/12. Moment d'inertie centrifuge: J xy = ∫xydF, si la section est symétrique à au moins un axe, J x y = 0. Le moment d'inertie centrifuge des corps asymétriques sera positif si la majeure partie de la zone est située dans les 1er et 3e quadrants. Moment d'inertie polaire: J ρ = ∫ρ 2 dF, ρ 2 = x 2 + y 2, où est la distance du centre des coordonnées à dF. J = J x + J y. Pour un cercle J ρ = πd 4/32, J x = πd 4/64. Pour l'anneau J ρ = 2J x = (D 4 -d 4) / 32 = πD 4 (1-α 4) / 32. Moments de résistance: pour un rectangle W x = J x / y max, où y max est la distance entre le centre de gravité de la section et les limites le long de y. W x = bh 2/6, W x = hb 2/6, pour un cercle W = J ρ / ρ max, W ρ = πd 3/16, pour un anneau W ρ = πD 3 (1-α 3) / 16 ... Coordonnées du centre de gravité: x c = (x1F1 + x2F2 + x3F3) / (F1 + F2 + F3). Rayons de giration principaux : i U = J U / F, i V = √J V / F. Moments d'inertie pour la translation parallèle des axes de coordonnées : J x 1 = J x c + b 2 F, J y 1 = J uc + a 2 F, J x 1 y 1 = J x cyc + abF.
7. Déformation par cisaillement et torsion. Changement pur un tel état de contraintes est appelé lorsque seules des contraintes tangentielles apparaissent sur les faces de l'élément sélectionné. En dessous de torsion comprendre le type de mouvement, pour lequel un facteur de force Mz ≠ 0 apparaît dans la section transversale de la tige, le reste Mx = My = 0, N = 0, Qx = Qy = 0. L'évolution des facteurs de force internes le long de la longueur est représentée sous la forme d'un diagramme en utilisant la méthode de la section et la règle du signe. Lors de la déformation par cisaillement, la contrainte de cisaillement τ est liée à la déformation angulaire γ par la relation τ = Gγ. dφ / dz = - angle de torsion relatif C'est l'angle de rotation mutuelle de deux sections, rapporté à la distance qui les sépare. θ = М К / GJ ρ, où GJ ρ est la rigidité en torsion de la section transversale. τ max = M Kmax / W ρ ≤ [τ] est la condition de résistance à la torsion des barres rondes. θ max = М К / GJ ρ ≤ [θ] - la condition pour la rigidité en torsion des tiges rondes. [θ] - dépend du type de supports.
8. Plier. En dessous de pliez comprendre ce type de chargement, auquel l'axe de la tige est plié (courbé) sous l'action de charges situées perpendiculairement à l'axe. Les arbres de toutes les machines sont soumis à une flexion due à l'action de forces, une paire de forces - le moment aux points d'atterrissage des roues dentées, des engrenages, des demi-accouplements. 1) Nom du pli nettoyer si un seul facteur de force apparaît dans la section transversale de la barre - un moment de flexion, les facteurs de force internes restants sont égaux à zéro. La formation de contraintes lors d'un pliage pur peut être considérée comme le résultat de la rotation des sections transversales plates les unes par rapport aux autres. σ = М у / J x - Formule de Navier pour la détermination des contraintes. ε = у / ρ - déformation relative longitudinale. Différence de dépendance : q = dQz / dz, Qz = dMz / dz. Condition de résistance : σ max = M max / W x ≤ [σ] 2) Nom du pli appartement si le plan de force, c'est-à-dire le plan d'action des charges coïncide avec l'un des axes centraux. 3) Nommer le pli oblique si le plan d'action des charges ne coïncide avec aucun des axes centraux. Le lieu des points de la section, satisfaisant la condition σ = 0, est appelé ligne de section neutre, il est perpendiculaire au plan de courbure de la barre courbe. 4) Nommer le pli transversal si un moment fléchissant et une force de cisaillement se produisent dans la section transversale. τ = QS x ab / bJ x est la formule de Zhuravsky, τ max = Q max S xmax / bJ x ≤ [τ] est la condition de résistance. Un contrôle complet de la résistance des poutres en flexion transversale consiste à déterminer les dimensions de la section transversale à l'aide de la formule de Navier et à vérifier davantage les contraintes de cisaillement. Parce que la présence de τ et dans la section fait référence à un chargement complexe, alors l'évaluation de l'état de contrainte sous leur action conjointe peut être calculée en utilisant la théorie de résistance 4 σ eq4 = √σ 2 + 3τ 2 ≤ [σ].
9. État tendu.Étudions l'état de contrainte (NS) au voisinage du point A, pour cela nous sélectionnons un parallélépipède infiniment petit, que nous plaçons à une échelle agrandie dans le système de coordonnées. Nous remplaçons les actions de la partie rejetée par des facteurs de force internes, dont l'intensité peut être exprimée par le vecteur principal des contraintes normales et tangentielles, que nous développons le long de trois axes - ce sont les composantes de la NS du point A. Peu importe quelle que soit la difficulté de chargement du corps, il est toujours possible de distinguer des zones perpendiculaires entre elles , pour lesquelles les contraintes de cisaillement sont égales à zéro. Ces sites sont appelés les principaux. NS linéaire - lorsque σ2 = σ3 = 0, NS plat - lorsque σ3 = 0, NS en vrac - lorsque σ1 ≠ 0, σ2 ≠ 0, σ3 ≠ 0. σ1, σ2, σ3 - contraintes principales. Contraintes sur les zones inclinées au PNS : τ β = -τ α = 0,5 (σ2-σ1) sinα, σ α = 0,5 (σ1 + σ2) +0,5 (σ1-σ2) cos2α, σ β = σ1sin 2 α + σ2cos 2 α .
10. La théorie de la force. Dans le cas du LNS, l'évaluation de la résistance est effectuée selon la condition σ max = σ1≤ [σ] = σ avant / [n]. En présence de σ1> σ2> σ3, dans le cas de NS, la détermination expérimentale de l'état dangereux est laborieuse en raison du grand nombre d'expériences avec diverses combinaisons de contraintes. On utilise donc un critère qui permet de distinguer l'influence prédominante d'un des facteurs, qui sera appelé critère et constituera la base de la théorie. 1) la première théorie de résistance (contraintes normales les plus élevées) : les états de contraintes sont égaux à la rupture fragile s'ils ont des contraintes de traction égales (ne prend pas en compte σ2 et σ3) - σ eq = σ1≤ [σ]. 2) la deuxième théorie de la résistance (les plus grandes déformations en traction - t Mariotte) : les sost n6contraintes sont également fortes pour la rupture fragile, si elles présentent les plus grandes déformations en traction. ε max = ε1≤ [ε], ε1 = (σ1-μ (σ2 + σ3)) / E, σeq = σ1-μ (σ2 + σ3) ≤ [σ]. 3) la troisième théorie de la résistance (contrainte maximale - Coulomb) : les contraintes sont égales en résistance selon l'apparition de déformations plastiques inacceptables, si elles ont la contrainte maximale τ max = 0,5 (σ1-σ3) ≤ [τ] = [σ ] / 2, eq = σ1-σ3≤ [σ] σ eq = √σ 2 + 4τ 2 [σ]. 4) la quatrième théorie de l'énergie potentielle spécifique de changement de forme (énergétique) : lors de la déformation du potentiel, la consommation d'énergie pour changer la forme et le volume U = U f + UV est sollicitée avec une force égale en fonction de l'apparition de plastique inacceptable déformations, si elles ont des potentiels spécifiques égaux de l'énergie de changement de forme. U éq = U f. Compte tenu du z-on généralisé de Hooke et des mathématiques des transformations σ eq = √ (σ1 2 + σ2 2 + σ3 2 -σ1σ2-σ2σ3-σ3σ1) ≤ [σ], σ eq = √ (0.5 [(σ1-σ2 ) 2 + (σ1-σ3) 2 + (σ3-σ2) 2]) [τ]. Dans le cas du PNS, σeq = √σ 2 + 3τ 2. 5) Cinquième théorie de la résistance de Mohr (généralisation de la théorie des états limites) : l'état limite dangereux est déterminé par deux contraintes principales, naib et naim eq = σ1-kσ3≤ [σ], où k est le coefficient de résistance inégale , qui prend en compte la capacité du matériau à résister à l'étirement et à la compression de manière inégale à = [σ p] / [σ comp].
11. Théorèmes de l'énergie. Mouvement de flexion- dans les calculs d'ingénierie, il existe des cas où les poutres, satisfaisant la condition de résistance, n'ont pas une rigidité suffisante. La raideur ou la déformabilité de la poutre est déterminée par les déplacements : θ - angle de rotation, - déflexion. Sous charge, la poutre se déforme et est une ligne élastique, qui se déforme le long du rayon ρ A. La flèche et l'angle de rotation en t A sont formés par la ligne élastique tangente de la poutre et l'axe z. Calculer la rigidité signifie déterminer la déflexion maximale et la comparer avec celle admissible. La méthode de Mohr- une méthode universelle de détermination des déplacements pour des systèmes planaires et spatiaux à raideur constante et variable, pratique car programmable. Pour déterminer la déflexion, dessinez une poutre fictive et appliquez une force unitaire sans dimension. = 1 / EJ x * ∑∫MM 1 dz. Pour déterminer l'angle de rotation, dessinez une poutre fictive et appliquez un moment sans dimension unitaire θ = 1 / EJ x * ∑∫MM '1 dz. La règle de Verechtchaguine- c'est pratique car, à raideur constante, l'intégration peut être remplacée par la multiplication algébrique des diagrammes des moments fléchissants de la charge et de la composition unitaire de la poutre. La méthode principale Yavl, qui est utilisée dans la divulgation du SNA. Δ = 1 / EJ x * ∑ω p M 1 c - Règle de Vereshchagin, dans laquelle le déplacement est inversement proportionnel à la rigidité de la poutre et est directement proportionnel au produit de la surface de la poutre de charge par l'ordonnée de la centre de gravité. Caractéristiques d'application : le diagramme des moments fléchissants est découpé en figures élémentaires, ω p et M 1 c sont pris en compte en tenant compte des signes, si q et P ou R agissent simultanément sur la section, alors les diagrammes doivent être délaminés, c'est-à-dire construire séparément de chaque charge ou appliquer différentes techniques de stratification.
12. Systèmes statiquement indéterminés. SNS est appelé le système, pour lequel les équations de la statique ne suffisent pas à déterminer les réactions des supports, c'est-à-dire il y a plus de connexions, de réactions qu'il n'en faut pour leur équilibre. La différence entre le nombre total de supports et le nombre d'équations statiques indépendantes, qui peuvent être compilées pour un système donné le degré d'incertitude statiqueS. Les liens imposés au système de supernécessaire sont dits superflus ou additionnels. L'introduction de fixations d'appui supplémentaires entraîne une diminution des moments de flexion et de la flèche maximale, c'est-à-dire la résistance et la rigidité de la structure augmentent. Pour révéler l'indétermination statique, une condition supplémentaire de compatibilité de déformation est ajoutée, qui permet la détermination de réactions d'appui supplémentaires, puis la décision sur la détermination des diagrammes Q et M est effectuée comme d'habitude. Système principal est obtenu à partir de celui donné en éliminant les connexions et les charges inutiles. Système équivalent- est obtenu en chargeant le système principal de charges et de réactions inconnues inutiles remplaçant les actions de la connexion rejetée. En utilisant le principe d'indépendance de l'action des forces, on trouve la flèche de la charge P et la réaction x1. σ 11 x 1 + Δ 1р = 0 est l'équation canonique de compatibilité de déformation, où 1р est le déplacement au point d'application x1 de la force P. Δ 1р - Мр * М1, σ 11 -М1 * М1 - c'est pratique pour effectuer cela par la méthode de Vereshchagin. Vérification de la déformation de la solution- pour cela, nous sélectionnons un autre système de base et, après avoir déterminé l'angle de rotation dans le support, doit être égal à zéro, θ = 0 - M ∑ * M ’.
13. Force cyclique. Dans la pratique de l'ingénierie, jusqu'à 80 % des pièces de la machine échouent en raison de la résistance statique à des contraintes bien inférieures à σ dans les cas où les contraintes sont alternées et changent de manière cyclique. Le processus d'accumulation de dommages lors de changements cycliques. le stress est appelé fatigue matérielle. Le processus de résistance à la fatigue est appelé force cyclique ou endurance. Période T du cycle. max τmax sont des contraintes normales. m, m - contrainte moyenne ; r-coefficient d'asymétrie du cycle ; facteurs affectant la limite d'endurance : a) Concentrateurs de tension : rainures, congés, clés, filetages et cannelures ; ceci est pris en compte par les coefficients effectifs de contraintes d'extrémité, qui sont notés K σ = σ -1 / σ -1k K τ = τ -1 / τ -1k ; b) Rugosité de surface : plus l'usinage du métal est rugueux, plus il y a de défauts métalliques lors de la coulée, plus la limite d'endurance de la pièce sera basse. Toute microfissure ou indentation après la fraise peut être à l'origine d'une fissure de fatigue. Ceci est pris en compte par le coefficient d'influence de la qualité de surface. Fσ К Fτ - ; c) Le facteur d'échelle affecte la limite d'endurance, avec une augmentation de la taille de la pièce, la probabilité de défauts augmente, par conséquent, plus la taille de la pièce est grande, plus mauvaise est l'évaluation de son endurance, cela prend en compte le coefficient de influence des dimensions absolues de la section transversale. K dσ K dτ. Coefficient défectueux : K σD = / Kv ; Kv - le facteur de durcissement dépend du type de traitement thermique.
14. Durabilité. La transition d'un système d'un état stable à un état instable est appelée une perte de stabilité, et la force correspondante est appelée force critique р En 1774, E. Euler mena une étude et détermina mathématiquement Rcr. Selon Euler, Rcr est la force requise pour la plus petite inclinaison de la colonne. Rcr = P 2 * E * Imin / L 2; Flexibilité de la tige= * L / i min; Stress critique cr = P 2 E / 2. Flexibilité ultime ne dépend que des propriétés physiques et mécaniques du matériau de la tige et il est constant pour un matériau donné.
La résistance des matériaux- une section de mécanique des solides, qui considère les méthodes de calcul des éléments des machines et des structures pour la résistance, la rigidité et la stabilité.
La résistance est la capacité d'un matériau à résister aux forces extérieures sans s'effondrer et sans l'apparition de déformations permanentes. Les calculs de résistance permettent de déterminer la taille et la forme des pièces pouvant supporter une charge donnée au moindre coût matière.
La rigidité est la capacité d'un corps à résister à la déformation. Les calculs de rigidité garantissent que les changements dans la forme et la taille du corps ne dépassent pas les limites acceptables.
La résilience est la capacité des structures à résister aux efforts qui tendent à les déséquilibrer. Les calculs de stabilité empêchent la perte soudaine d'équilibre et la distorsion des éléments structurels.
La durabilité consiste en la capacité d'une structure à maintenir les propriétés de service nécessaires à son fonctionnement pendant une période de temps prédéterminée.
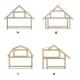
Une barre (Fig. 1, a - c) est un corps dont les dimensions transversales sont petites par rapport à la longueur. L'axe de la barre est la ligne reliant les centres de gravité de ses sections transversales. Distinguer les barres de section constante ou variable. Le faisceau peut avoir un axe droit ou courbe. Une barre à axe rectiligne est appelée barre (Fig. 1, a, b). Les éléments structurels à parois minces sont divisés en plaques et coques.
La coque (Fig. 1, d) est un corps dont l'une des dimensions (épaisseur) est beaucoup plus petite que les autres. Si la surface de la coque est un plan, alors l'objet est appelé plaque (Fig. 1, e). Les corps sont appelés corps dans lesquels toutes les tailles sont du même ordre (Fig. 1, f). Il s'agit notamment des fondations des structures, des murs de soutènement, etc.
Ces éléments de la résistance des matériaux permettent d'établir un schéma de conception d'un objet réel et de conduire son analyse technique. Un schéma de conception est compris comme un certain modèle idéalisé d'une structure réelle, dans lequel tous les facteurs insignifiants affectant son comportement sous charge sont rejetés.
Hypothèses de propriétés matérielles
Le matériau est considéré comme solide, homogène, isotrope et idéalement élastique.
Continuité - le matériau est considéré comme continu. Homogénéité - Les propriétés physiques d'un matériau sont les mêmes en tout point.
Isotropie - les propriétés des matériaux sont les mêmes dans toutes les directions.
Élasticité parfaite- la propriété d'un matériau (corps) à restaurer complètement sa forme et sa taille après avoir éliminé les causes de déformation.
Hypothèses de souche
1. L'hypothèse de l'absence d'efforts internes initiaux.
2. Le principe d'invariabilité des dimensions initiales - les déformations sont faibles par rapport aux dimensions originales du corps.
3. L'hypothèse de déformabilité linéaire des corps - les déformations sont directement proportionnelles aux forces appliquées (loi de Hooke).
4. Le principe de l'indépendance de l'action des forces.
5. Hypothèse des sections plates de Bernoulli - les sections plates du bois avant déformation restent planes et normales à l'axe du bois après déformation.
6. Le principe de Saint-Venant - l'état de contrainte du corps à une distance suffisante de la zone d'action des charges locales dépend très peu de la méthode détaillée de leur application
Forces externes
L'action sur la structure des corps environnants est remplacée par des forces appelées forces ou charges externes. Considérons leur classification. Les charges comprennent des forces actives (pour la perception desquelles la structure a été créée) et réactives (réactions de liaison) - des forces qui équilibrent la structure. Selon la méthode d'application, les forces externes peuvent être divisées en concentrées et réparties. Les charges réparties sont caractérisées par l'intensité et peuvent être linéaires, superficielles ou volumétriques. De par la nature de l'impact de la charge, les forces externes sont statiques et dynamiques. Les forces statiques comprennent des charges dont les changements dans le temps sont faibles, c'est-à-dire les accélérations de points d'éléments structuraux (forces d'inertie) peuvent être négligées. Les charges dynamiques provoquent de telles accélérations dans la structure ou ses éléments individuels, qui ne peuvent être négligées dans les calculs.
Forces internes. Méthode des sections.
L'action de forces externes sur le corps entraîne sa déformation (l'arrangement mutuel des particules corporelles change). En conséquence, des forces d'interaction supplémentaires apparaissent entre les particules. Ce sont les forces de résistance aux changements de forme et de taille du corps sous l'action d'une charge, appelées forces internes (efforts). Avec l'augmentation de la charge, les efforts internes augmentent. La rupture d'un élément structurel se produit lorsque les forces externes dépassent un certain niveau maximum de forces internes pour une structure donnée. Par conséquent, l'évaluation de la résistance d'une structure chargée nécessite la connaissance de l'amplitude et de la direction des efforts internes résultants. Les valeurs et les directions des forces internes dans un corps chargé sont déterminées pour des charges externes données par la méthode de la section.
La méthode de section (voir Fig. 2) consiste dans le fait qu'une barre en équilibre sous l'action d'un système de forces externes est mentalement coupée en deux parties (Fig. 2, a), et l'équilibre de l'une d'entre elles est considéré , remplaçant l'action de la partie écartée de la barre par un système d'efforts internes répartis sur la section (Fig. 2, b). Notez que les efforts internes pour la barre dans son ensemble deviennent externes pour l'une de ses parties. De plus, dans tous les cas, les efforts internes équilibrent les efforts externes agissant sur la partie coupée de la barre.
Conformément à la règle du transfert parallèle des forces statiques, nous ramenons toutes les forces internes réparties au centre de gravité de la section. On obtient ainsi leur vecteur principal R et leur moment principal M du système de forces internes (Fig. 2, c). En choisissant un repère O xyz pour que l'axe z soit l'axe longitudinal de la barre et en projetant le vecteur principal R et le moment principal M des efforts internes sur l'axe, on obtient six facteurs d'efforts internes dans la section de la barre : effort longitudinal N , les efforts transversaux Q x et Q y, les moments fléchissants M x et M y, ainsi que le couple T. Par le type de facteurs de force internes, il est possible de déterminer la nature du chargement de la poutre. Si seule la force longitudinale N apparaît dans les sections transversales de la poutre et qu'il n'y a pas d'autres facteurs de force, il y a alors un "étirement" ou une "compression" de la poutre (selon la direction de la force N). Si seul l'effort tranchant Q x ou Q y agit dans les sections, c'est le cas du « cisaillement pur ». En cas de « torsion » dans les sections de la barre, seuls agissent les couples T. En « flexion pure » - seuls les moments de flexion M. Des types de chargement combinés (flexion avec traction, torsion avec flexion, etc.) sont également possibles - ce sont des cas de "résistance complexe". Pour une représentation visuelle de la nature de l'évolution des facteurs de force internes le long de l'axe de la barre, leurs graphiques sont construits, appelés diagrammes. Les schémas permettent de déterminer les sections de poutre les plus chargées et d'établir les sections dangereuses.
8.2. Lois fondamentales utilisées dans la résistance des matériaux
Relations statiques. Elles s'écrivent sous la forme des équations d'équilibre suivantes.
la loi de Hooke ( 1678): plus la force est grande, plus la déformation est grande et, en proportion directe de la force... Physiquement, cela signifie que tous les corps sont des ressorts, mais avec une grande rigidité. Avec un simple étirement d'une barre avec une force longitudinale N= F cette loi peut s'écrire :
Ici 
force longitudinale, je- la longueur de la barre, UNE- sa section transversale, E- coefficient d'élasticité du premier type ( Module d'Young).
En tenant compte des formules des contraintes et des déformations, la loi de Hooke s'écrit comme suit : 
.
Une relation similaire est observée dans les expériences entre les contraintes de cisaillement et l'angle de cisaillement :
.
g
sont appelésmodule de cisaillement
, moins souvent - le module d'élasticité du deuxième type. Comme toute loi, la loi de Hooke a une limite d'applicabilité. Tension 
, à laquelle la loi de Hooke est valide, est appelé limite proportionnelle(c'est la caractéristique la plus importante dans les matériaux de résistance).
Représentons la dépendance
à partir de
graphiquement (Figure 8.1). Ce tableau s'appelle diagramme d'étirement
... Après le point B (c'est-à-dire à 
) cette dépendance cesse d'être simple.
À 
après déchargement, des déformations résiduelles apparaissent dans la caisse, donc 
appelé limite élastique
.
Lorsque la contrainte atteint σ = σt, de nombreux métaux commencent à présenter une propriété appelée fluidité... Cela signifie que même sous une charge constante, le matériau continue de se déformer (c'est-à-dire qu'il se comporte comme un liquide). Graphiquement, cela signifie que le diagramme est parallèle à l'abscisse (section DL). La contrainte t à laquelle le matériau s'écoule est appelée seuil de rentabilité .
Certains matériaux (Art. 3 - acier de construction), après un court écoulement, recommencent à résister. La résistance du matériau se poursuit jusqu'à une certaine valeur maximale de pr, puis la destruction progressive commence. La valeur de pr - est appelée force ultime (synonyme pour l'acier : résistance à la traction, pour le béton - résistance cubique ou prismatique). Les désignations suivantes sont également utilisées :
=R b
Une relation similaire est observée dans les expériences entre les contraintes de cisaillement et les cisaillements.
3) Loi de Duhamel-Neumann (dilatation thermique linéaire) :
En présence d'une baisse de température, les corps changent de taille, et en proportion directe de cette baisse de température.
Qu'il y ait une différence de température 
... Alors cette loi a la forme :
Ici α - coefficient de dilatation thermique linéaire, je - longueur de tige, je- son allongement.
4) Loi sur le fluage .
La recherche a montré que tous les matériaux sont très hétérogènes dans les petites choses. La structure schématique de l'acier est illustrée à la figure 8.2.
Certains des constituants ont des propriétés liquides, de sorte que de nombreux matériaux sous charge obtiendront un allongement supplémentaire au fil du temps. 
(Figure 8.3.) (métaux à haute température, béton, bois, plastiques à température normale). Ce phénomène est appelé ramper Matériel.
Pour un liquide, la loi est vraie : plus la force est grande, plus la vitesse de déplacement du corps dans le fluide est grande... Si ce rapport est linéaire (c'est-à-dire que la force est proportionnelle à la vitesse), alors vous pouvez l'écrire sous la forme :
E 
Si nous allons aux forces relatives et aux allongements relatifs, nous obtenons
Ici l'indice " cr
« signifie que l'on considère la partie de l'allongement qui est causée par le fluage du matériau. Caractéristique mécanique 
appelé coefficient de viscosité.
Loi de conservation de l'énergie.
Considérez une barre chargée
Introduisons le concept de déplacement d'un point, par exemple,
- mouvement vertical du point B ;
- déplacement horizontal du point C.
Les forces 
faire du travail U.
Étant donné que les forces 
commencent à augmenter progressivement et en supposant qu'ils augmentent proportionnellement aux déplacements, on obtient :
.
Selon la loi de conservation : aucun travail ne disparaît, il est dépensé pour faire un autre travail ou passe dans une autre énergie (énergie est le travail que le corps peut faire.)
Forces de travail 
, est consacré à surmonter la résistance des forces élastiques qui surviennent dans notre corps. Pour calculer ce travail, prenons en compte que le corps peut être considéré comme constitué de petites particules élastiques. Considérons l'un d'eux :
Du côté des particules voisines, une tension agit sur elle 
... Les contraintes résultantes seront 
Sous l'influence 
la particule s'allongera. L'allongement est défini comme l'allongement par unité de longueur. Puis:
Calculons le travail dW que la force fait dN (ici, il est également pris en compte que les forces dN commencent à augmenter progressivement et elles augmentent proportionnellement aux déplacements) :
Pour l'ensemble du corps on obtient :
.
Travail W qui a été commis 
sont appelés énergie de déformation élastique.
D'après la loi de conservation de l'énergie :
6)Principe mouvements possibles .
C'est l'une des options pour enregistrer la loi de conservation de l'énergie.
Laissez les forces agir sur la barre F 1
,
F 2
,
…
... Ils provoquent le déplacement de points dans le corps. 
et tension 
... Donnons le corps petits déplacements supplémentaires possibles
... En mécanique, un enregistrement de la forme 
signifie l'expression "valeur possible de la quantité une". Ces mouvements possibles provoqueront dans le corps déformations supplémentaires possibles
... Ils conduiront à l'apparition de forces et de contraintes externes supplémentaires. 
,
δ.
Calculons le travail des forces extérieures sur les petits déplacements supplémentaires possibles :
Ici 
- déplacements supplémentaires des points auxquels les forces sont appliquées F 1
,
F 2
,
…
Considérons à nouveau un petit élément avec une section transversale dA et longueur dz (voir fig. 8.5. et 8.6.). Par définition, un allongement supplémentaire dz de cet élément est calculé par la formule :
dz= dz.
La force de traction de l'élément sera :
dN = (+δ) dA ≈ dA..
Le travail des efforts internes sur les déplacements supplémentaires est calculé pour un petit élément comme suit :
dW = dN dz = dA dz = dV
AVEC 
En additionnant l'énergie de déformation de tous les petits éléments, nous obtenons l'énergie de déformation totale :
Loi de conservation de l'énergie W = U donne :
.
Ce rapport est appelé principe de déplacement possible(aussi appelé principe des mouvements virtuels). De même, nous pouvons considérer le cas où des contraintes tangentielles agissent également. On obtient alors que l'énergie de déformation W le terme suivant est ajouté :
Ici est la contrainte de cisaillement, est le cisaillement d'un petit élément. Puis principe des déplacements possibles prendra la forme :
Contrairement à la forme précédente d'écriture de la loi de conservation de l'énergie, il n'y a aucune hypothèse ici que les forces commencent à augmenter progressivement, et elles augmentent proportionnellement aux déplacements
7) effet Poisson.
Considérez l'image de l'allongement de l'échantillon :
Le phénomène de raccourcissement d'un élément du corps dans le sens de l'allongement est appelé effet Poisson.
Trouvons la déformation relative longitudinale.
La déformation relative transversale sera :
Coefficient de Poisson la quantité s'appelle :
Pour les matériaux isotropes (acier, fonte, béton) Coefficient de Poisson
Cela signifie que dans le sens transversal, la déformation moins longitudinal.
Noter
: les technologies modernes peuvent créer des matériaux composites avec un coefficient de Poisson > 1, c'est-à-dire que la déformation transversale sera supérieure à la déformation longitudinale. C'est par exemple le cas d'un matériau renforcé de fibres rigides à faible inclinaison 
<<1
(см. рис.8.8.). Оказывается, что коэффициент
Пуассона при этом почти пропорционален
величине
, c'est à dire. le moins 
, plus le coefficient de Poisson est grand.
Graphique 8.8. Graphique 8.9
Encore plus surprenant est le matériau montré dans (Figure 8.9.), Et pour un tel renforcement, un résultat paradoxal a lieu - l'allongement longitudinal conduit à une augmentation de la taille du corps dans le sens transversal.
8) La loi de Hooke généralisée.
Considérons un élément qui est étiré longitudinalement et transversalement. Trouvons la déformation qui se produit dans ces directions. 
Calculons la déformation 
découlant de l'action 
:
Tenir compte de la déformation due à l'action 
, qui se produit sous l'effet de l'effet Poisson :
La déformation globale sera :
Si valide et 
, puis ajoutez un raccourcissement supplémentaire dans la direction de l'axe x 
.
D'où: 
Également: 
Ces rapports sont appelés loi de Hooke généralisée.
Fait intéressant, lors de l'écriture de la loi de Hooke, une hypothèse est faite sur l'indépendance des déformations d'allongement des déformations de cisaillement (à propos de l'indépendance des contraintes de cisaillement, ce qui est le même) et vice versa. Les expériences confirment bien ces hypothèses. Pour l'avenir, nous notons que la résistance, au contraire, dépend fortement de la combinaison des contraintes de cisaillement et normales.
Noter: Les lois et hypothèses ci-dessus sont confirmées par de nombreuses expériences directes et indirectes, mais, comme toutes les autres lois, elles ont un domaine d'application limité.
